题目内容
【题目】如图所示,电脑绣花设计师准备在长120cm,宽8cm的矩形ABCD模板区域内设计绣花方案,现将其划分为区域Ⅰ(2个全等的五边形),区域Ⅱ(2个全等的菱形),区域Ⅲ(正方形EFGH中减去与2个菱形重合的部分),剩余为不刺绣的空白部分:点O是整副图形的对称中心EG∥AB,H,F分别为2个菱形的中心,MH=2PH,HQ=2OQ,为了美观,要求MT不超过10cm.若设OQ=x(cm),x为正整数.

(1)用含x的代数式表示区域Ⅲ的面积;
(2)当矩形ABCD内区域Ⅰ的面积最小时,图案给人的视觉感最好.求此时MN的长度;
(3)区域Ⅰ,Ⅱ,Ⅲ的刺绣方式各有不同.区域Ⅰ与区域Ⅲ所用的总针数之比为29:19,区域Ⅱ与区域Ⅲ每平方厘米所用的针数分别为a,b针(a,b均为整数,a>b),区域Ⅲ的面积为正整数.这时整个模板的总针数为12960针,则a+b= .
【答案】(1)![]() x2(cm2);(2)72cm;(3)5
x2(cm2);(2)72cm;(3)5
【解析】
(1)由题意根据区域Ⅲ的面积=正方形EFGH的面积﹣4×△JQH的面积进行分析求解;
(2)根据题意构建二次函数,求出自变量的取值范围即可解决问题;
(3)由(2)可知:7.5≤x<10,由区域Ⅲ的面积=![]() x2是整数,可得x=9,由区域Ⅰ与区域Ⅲ所用的总针数之比为29:19,可以假设区域Ⅰ与区域Ⅲ所用的总针数分别为29k,19k,由区域Ⅱ的面积=32x2,区域Ⅲ的面积=
x2是整数,可得x=9,由区域Ⅰ与区域Ⅲ所用的总针数之比为29:19,可以假设区域Ⅰ与区域Ⅲ所用的总针数分别为29k,19k,由区域Ⅱ的面积=32x2,区域Ⅲ的面积=![]() x2,设区域Ⅱ的总针数为y.则有
x2,设区域Ⅱ的总针数为y.则有![]() =
=![]() ,可得y=48k,根据整个模板的总针数为12960针,构建方程求出k,即可解决问题.
,可得y=48k,根据整个模板的总针数为12960针,构建方程求出k,即可解决问题.
解:(1)∵OQ=x,
∴HQ=2OQ=2x,OH=3x,HF=6x,
∴菱形EFGH的面积为18x2(cm2),
设EH交MQ于J.
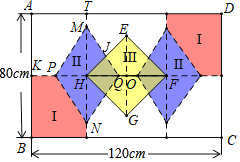
∵∠JHQ=45°,tan∠JQH=2,HQ=2x
解得这个三角形的面积为:![]() x2(cm2),
x2(cm2),
∴区域Ⅲ的面积为:18x2﹣4×![]() x2=
x2=![]() x2(cm2).
x2(cm2).
(2)令区域Ⅰ的面积为y,则y=2×[40(60﹣3x)﹣4x2]=﹣8x2﹣240x+4800,
∴该函数的对称轴为:直线x=﹣15,
∵a=﹣8<0,
∴在对称轴右侧y随x的增大而减小,
∵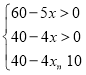 ,
,
∴7.5≤x<10,x为正整数,
∴x=8,9,
∴当x=9时,区域Ⅰ面积最小,此时MN=8x=72cm.
(3)由(2)可知:7.5≤x<10,
∵区域Ⅲ的面积=![]() x2是整数,
x2是整数,
∴x=9,
∵区域Ⅰ与区域Ⅲ所用的总针数之比为29:19,
∴可以假设区域Ⅰ与区域Ⅲ所用的总针数分别为29k,19k,
∵区域Ⅱ的面积=32x2,区域Ⅲ的面积=![]() x2,
x2,
设区域Ⅱ的总针数为y.则有![]() =
=![]() ,
,
∴y=48k,
∵整个模板的总针数为12960针,
∴29k+48k+19k=12960,
∴k=135,
∴a+b=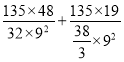 =5.
=5.
故答案为:5.

【题目】 黄石知名特产“黄石港饼”“白鸭牌松花皮蛋”“珍珠果米酒”一直以来享有美誉,深受人们喜爱.端午节快到了,为了满足市场需求,某公司组织20辆汽车装运港饼、皮蛋、米酒共120吨去外地销售,按计划20辆汽车都要装满,且每辆汽车只能装运同一类食品,根据下表提供的信息解答以下问题.
港饼 | 皮蛋 | 米酒 | |
每辆汽车载重量(吨) | 8 | 6 | 5 |
每吨食品获利(万元) | 0.2 | 0.4 | 0.6 |
(1)设装运港饼的车辆为x辆,装运皮蛋的车辆为y辆,求y与x之间的函数关系式;
(2)此次销售获利为W万元,试求W关于x的函数关系式;
(3)如果装运每种食品的车辆都不少于2辆,那么怎样安排车辆能使此次销售获利最大?并求出最大利润.