题目内容
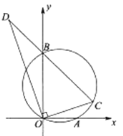
【题目】已知二次函数y=ax2+bx+c的图象顶点坐标为(1,4),且经过点C(3,0).
(1)求该二次函数的解析式;
(2)当x取何值时,y随x的增大而减小?
(3)当![]() 时,直接写出x的取值范围.
时,直接写出x的取值范围.
【答案】(1)![]() ;(2)当
;(2)当![]() 时y随x的增大而减小;(3)
时y随x的增大而减小;(3)![]() 或
或![]()
【解析】
(1)由于已知抛物线顶点坐标,则可设顶点式![]() ,然后把(3,0)代入求出a的值即可;
,然后把(3,0)代入求出a的值即可;
(2)根据二次函数的性质,当开口向下时,在对称轴右侧y随x的增大而减小,即![]() ;
;
(3)易证得抛物线与直线y=-x+3的交点为(0,3)和(3,0),根据解得坐标,结合二次函数的性质即可求得;
(1)设![]() ,将C(3,0)代入得a=-1,
,将C(3,0)代入得a=-1,
∴![]() ,
,
(2)∵![]() <0,
<0,
∴在对称轴的右边y随x的增大而减小,
∴当![]() 时y随x的增大而减小,
时y随x的增大而减小,
(3)抛物线![]() 中,顶点为(1,4),
中,顶点为(1,4),
令x=0,则y=3,
∴抛物线经过点(0,3),
令y=0,则x=3,
∴抛物线经过点(3,0),
由直线y=-x+3可知,直线也经过点(3,0),点(0,3),
∵a=-1<0,
∴开口向下,
∴当![]() 时,x的取值范围为:
时,x的取值范围为:![]() 或
或![]() ;
;

练习册系列答案
相关题目
【题目】(探究与创新):已知A、B在数轴上分别表示a、b
①对照数轴填写下表:
a | 6 | ﹣6 | ﹣6 | 2 | ﹣1.5 |
b | 4 | 0 | ﹣4 | ﹣10 | ﹣1.5 |
A、B两点的距离 | 2 |
|
|
| 0 |
②若A、B两点间的距离记为d,则d和a、b之间有何数量关系?(直接写出结果)
③在数轴上标出所有符合条件的整数点P使它到5和﹣5的距离之和为10,并求出所有这些整数的和.
![]()
④若点Q表示的数为x,当点Q在什么位置时,|x+1|+|x﹣2|有最小值?最小值是多少?