Question

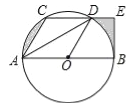
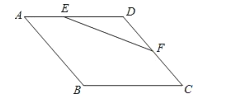
【题目】如图，菱形的边长为，，点是上一动点（不与、重合），点是上一动点，且，则面积的最大值为__________．

Answer 1

【答案】

【解析】

首先过点F作FG⊥AD，交AD的延长线于点G，由菱形ABCD的边长为4，∠BAD=60°，即可求得AD=CD=4，∠FDG=60°，然后设AE=x，即可得S△DEF=DEFG）=-（x-2）2+，然后根据二次函数的性质，即可求得答案．

解：过点F作FG⊥AD，交AD的延长线于点G，

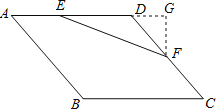
∵菱形ABCD边长为4，∠BAD=60°，
∴AD=CD=4，∠ADC=180°-∠BAD=120°，
∴∠FDG=180°-∠ADB=60°，
设AE=x，
∵AE+CF=4，
∴CF=4-x；
∴DE=AD-AE=4-x，DF=CD-CF=4-（4-x）=x，
在Rt△DFG中，FG=DFsin∠GDF=x，
∴S△DEF=DEFG=×（4-x）×x=-x2+x=-（x2-4x）=-（x-2）2+，
∴当x=2时，△DEF面积的最大，最大值为．
故答案为：．