题目内容
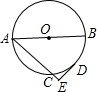 如图,AB是⊙O直径,AC是⊙O的弦,过弧BC的中点D作AC的垂线交AC的延长于E,若DE=2,EC=1,则⊙O的直径为
如图,AB是⊙O直径,AC是⊙O的弦,过弧BC的中点D作AC的垂线交AC的延长于E,若DE=2,EC=1,则⊙O的直径为
- A.

- B.

- C.5
- D.4
C
分析:连接OD,根据已知可推出四边形CFDE是矩形,再根据切割线定理求解即可.
解答: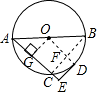 解:连接OD,
解:连接OD,
∵点D是弧BC的中点,
∴OD⊥BC,∠OFC=90°,AB是直径,
∴∠ACB=90°,DE⊥AE,
∴∠E=90°,
∴四边形CFDE是矩形,
∴∠ODE=90°,
∴ED是圆的切线.
作OG⊥AC,则OG=CF=ED=2.
∵DE2=EC•AE,
∴AE=4,AC=3,AE= ,
,
∴AO= ,
,
∴AB=5.
故选C.
点评:本题利用了勾股定理,垂径定理,切割线定理,切线的概念,矩形的判定和性质,直径对的圆周角是直角求解.
分析:连接OD,根据已知可推出四边形CFDE是矩形,再根据切割线定理求解即可.
解答:
 解:连接OD,
解:连接OD,∵点D是弧BC的中点,
∴OD⊥BC,∠OFC=90°,AB是直径,
∴∠ACB=90°,DE⊥AE,
∴∠E=90°,
∴四边形CFDE是矩形,
∴∠ODE=90°,
∴ED是圆的切线.
作OG⊥AC,则OG=CF=ED=2.
∵DE2=EC•AE,
∴AE=4,AC=3,AE=
 ,
,∴AO=
 ,
,∴AB=5.
故选C.
点评:本题利用了勾股定理,垂径定理,切割线定理,切线的概念,矩形的判定和性质,直径对的圆周角是直角求解.

练习册系列答案
相关题目
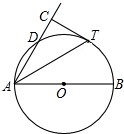 如图,AB是⊙O直径,D为⊙O上一点,AT平分∠BAD交⊙O于点T,过T作AD的垂线交AD的延长线于点C.
如图,AB是⊙O直径,D为⊙O上一点,AT平分∠BAD交⊙O于点T,过T作AD的垂线交AD的延长线于点C.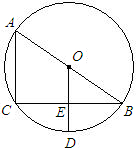 如图,AB是⊙O直径,BC是弦,OD⊥BC于E交弧BC于D.根据中考改编
如图,AB是⊙O直径,BC是弦,OD⊥BC于E交弧BC于D.根据中考改编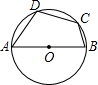 如图,AB是⊙O直径,C、D是⊙O上的两点,若∠BAC=20°,
如图,AB是⊙O直径,C、D是⊙O上的两点,若∠BAC=20°,
 如图,AB是⊙O直径,OB=6,弦CD=10,则弦心距OP的长为( )
如图,AB是⊙O直径,OB=6,弦CD=10,则弦心距OP的长为( ) 如图,AB是⊙O直径,弦CD交AB于E,∠AEC=45°,AB=2.设AE=x,CE2+DE2=y.下列图象中,能表示y与x的函数关系是的( )
如图,AB是⊙O直径,弦CD交AB于E,∠AEC=45°,AB=2.设AE=x,CE2+DE2=y.下列图象中,能表示y与x的函数关系是的( )