题目内容
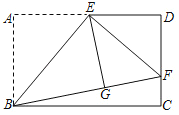
【题目】如图,在Rt△ABC中,∠BAC=90°,以AB为直径的⊙O交BC于点E,且点E是![]() 的中点,连接AD交BE于点F,连接EA,ED.
的中点,连接AD交BE于点F,连接EA,ED.
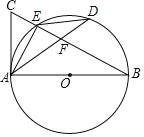
(1)求证:AC=AF;
(2)若EF=2,BF=8,求AF的长.
【答案】(1)证明见解析;(2)AF=![]()
【解析】
(1)根据等弧或同弧所对的圆周角相等、等腰三角形的性质及等角的余角相等即可得出答案;
(2)首先根据AB是⊙O的直径,得出AE⊥CF,再根据∠C=∠C,∠BAC=∠AEC=90°,得出△AEC∽△BAC,根据相似三角形的性质即可得出AC=![]() ,进一步可得出答案.
,进一步可得出答案.
(1)∵∠BAC=90°
∴∠C+∠ABC=90°
∵弧![]()
∴∠D=∠B
所以∠C+∠D=90°
∵E是![]() 的中点
的中点
∴![]()
∴∠EAD=∠D
∵AB是直径
∴∠AEF=90°
∴∠EAF+∠EFA=90°
∴∠D+∠EFA=90°
∴∠EFA=∠C
∴AC=AF
(2)∵AB是⊙O的直径
∴∠AEB=90°,即AE⊥CF
∵AC=AF,EF=2
∴CE=EF=2
∵BF=8
∴BC=BF+EF+CE=12
∵∠C=∠C,∠BAC=∠AEC=90°
∴△AEC∽△BAC
∴![]() ,即
,即![]()
∴AC2=24
∴AC=![]()
∵AC=AF
∴AF=![]()

【题目】在新冠疫情防控期间,某医疗器械商业集团新进了40台A型电子体温测量仪,60台B型电子体温测量仪,计划调配给下属的甲、乙两个连锁店销售,其中70台给甲连锁店,30台给乙连锁店.两个连锁店销售这两种测量仪每台的利润(元)如下表:
A型 | B型 | |
甲连锁店 | 200 | 170 |
乙连锁店 | 160 | 150 |
设集团调配给甲连锁店![]() 台A型测量仪,集团卖出这100台测量仪的总利润为
台A型测量仪,集团卖出这100台测量仪的总利润为![]() (元).
(元).
(1)求![]() 关于
关于![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的取值范围:
的取值范围:
(2)为了促销,集团决定仅对甲连锁店的A型测量仪每台让利![]() 元销售,其他的销售利润不变,并且让利后每台A型测量仪的利润仍然高于甲连锁店销售的每台B型测量仪的利润,问该集团应该如何设计调配方案,使总利润达到最大?
元销售,其他的销售利润不变,并且让利后每台A型测量仪的利润仍然高于甲连锁店销售的每台B型测量仪的利润,问该集团应该如何设计调配方案,使总利润达到最大?