题目内容
【题目】已知点![]() ,
,![]() ,
,![]() ,
,![]() ,动点
,动点![]() 以每秒
以每秒![]() 个单位长度的速度沿
个单位长度的速度沿![]() 运动(
运动(![]() 不与点
不与点![]() ,
,![]() 重合),设运动时间为
重合),设运动时间为![]() 秒.
秒.
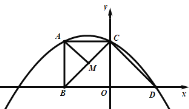
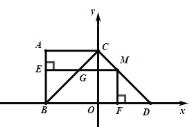
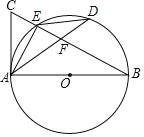
图(1) 图(2)
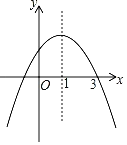
(1)求经过![]() ,
,![]() ,
,![]() 三点的抛物线的函数表达式;
三点的抛物线的函数表达式;
(2)点![]() 在(1)中的抛物线上,当
在(1)中的抛物线上,当![]() 为
为![]() 的中点时,若
的中点时,若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)当![]() 在
在![]() 上运动时,如图(2),过点
上运动时,如图(2),过点![]() 作
作![]() 轴,
轴,![]() ,垂足分别为
,垂足分别为![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() ,设矩形
,设矩形![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() ,当
,当![]() 为何值时,
为何值时,![]() 最大,最大值是多少?
最大,最大值是多少?
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)当
;(3)当![]() 时,
时,![]() 取得最大值为
取得最大值为![]()
【解析】
(1)设函数解析式为y=ax2+bx+c,将点A(-2,2),C(0,2),D(2,0)代入解析式即可;
(2)由已知易得点P为AB的垂直平分线与抛物线的交点,点P的纵坐标是1,代入解析式问题可解;
(3)分别用t表示GM、BF、MF表示面积,则问题可解.
解:(1)设抛物线的函数表达式为![]() ,则
,则
![]()
解这个方程组,得
![]()
(2)![]()
![]() ,
,![]()
![]() 点为线段
点为线段![]() 的垂直平分线与抛物线的交点
的垂直平分线与抛物线的交点
![]() 点
点![]() 的纵坐标为
的纵坐标为![]()
由![]() ,
,
得![]() ,
,![]()
所以点![]() 的坐标为
的坐标为![]() 或
或![]()
(3)![]() ,
,
![]()
![]()
![]()
![]()
![]()
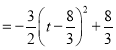 ,又
,又![]()
所以当![]() 时,
时,![]() 取得最大值为
取得最大值为![]()
【点解】
本题考查二次函数综合;熟练应用待定系数法求函数解析式,掌握三角形全等的性质,直线交点的求法是解题的关键.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目