Question

【题目】如图，在菱形ABCD中，AB=2，∠ABC=60°，对角线AC、BD相交于点O，将对角线AC所在的直线绕点O顺时针旋转角α（0°<α<90°）后得直线l，直线l与AD、BC两边分别相交于点E和点F．

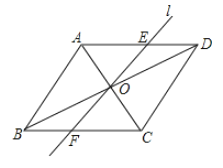
（1）求证：△AOE≌△COF；

（2）当α=30°时，求线段EF的长度．

Answer 1

【答案】（1）见解析；（2）

【解析】

（1）根据菱形得到AO=CO AD∥BC，根据平行线的性质得到∠OAE=∠OCF，结合对顶角得到三角形全等；

（2）根据菱形得出AB=BC=2，∠ABC=60°得到△ABC为等边三角形，根据题意得出OC=1，根据∠α=30°得出OF⊥BC，根据Rt△OFC得出OF的长度，根据全等得出EF=2OF得出答案．

（1）∵ABCD为菱形

∴AO=CO AD∥BC

∴∠OAE=∠OCF

又∵∠AOE=∠COF

∴△AOE≌△COF

（2）∵AB=BC=2，∠ABC=60°

∴△ABC为等边三角形

∵AC=2，∠ACB=60°

∴OC=1

当∠α=30°

∴OF⊥BC

在Rt△OFC中 ∠COF=30°

∴OF=OC=

又由（1）可得：OE=OF ∴EF=2OF=．