题目内容
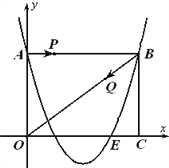
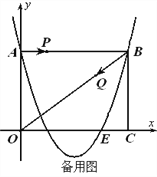
【题目】如图,在平面直角坐标系中,四边形OABC是矩形,OA=3,AB=4,将线段OA绕点O顺时针旋转90°,使点A落在OC边上的点E处,抛物线y=ax2+bx+c过A、E、B三点.
(1)求抛物线的解析式;
(2)若M为抛物线的对称轴上一动点,当△MBE的周长最小时,求M点的坐标;
(3)点P从A点出发,以每秒1个单位长度的速度沿AB向B点运动,同时点Q从点B出发,以每秒1个单位长度的速度沿BO向点O运动.P点到达终点B时,Q点同时停止运动,运动时间为t(秒).若△PBQ是等腰三角形,求![]() 的值.
的值.
【答案】(1)y=x2-4x+3(2)(2,1)(3)2, ![]() ,
, ![]()
【解析】试题分析:(1)先求出A、B、E三点坐标,再将A、B、E三点坐标代入y=ax2+bx+c即可求得抛物线的解析式;(2)由题意可知:M为直线AE与对称轴x=2的交点时,△MBE的周长最小,先求出直线AE的解析式,进而可求得点M的坐标;(3)根据题意,△DPQ为等腰三角形,可能有三种情形,需要分类讨论:①若PD=PQ;②若PD=DQ;③若PQ=DQ.
试题解析:
(1)∵四边形OABC是矩形,OA=3,AB=4,∴∠OAB=∠OCB=90°,OC=AB=4,CB=OA=3.又∵OE=OA=3,
∴A﹙0,3﹚,B﹙4,3﹚,E﹙3,0﹚∵抛物线y=ax2+bx+c经过A,B,E三点,∴
解之得: 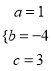
∴抛物线的解析式为:y=x2-4x+3.
(2)∵y=x2-4x+3=(x-2)2-1,
∴抛物线的对称轴为直线x=2.
∵点A,B关于直线x=2对称,∴M为直线AE与对称轴x=2的交点时,ME+MB的值最小,而BE的长一定,此时△MBE的周长最小.
设直线AE的解析式为y=kx+m,则有
![]()
解得![]() ∴y=-x+3.
∴y=-x+3.
当x=2时,y=1,
∴M点的坐标为(2,1)
(3)①若BP=BQ,则4-t=t,t=2
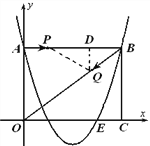
②若QP=QB,作QD⊥AB于D,则BD=![]() (4-t),
(4-t),
由![]() (4-t):4=t:5得t=
(4-t):4=t:5得t=![]()
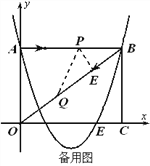
③若QP=PB,作PE⊥QB于E,则BE=![]() t,
t,
由(4-t):5=![]() t:4得t=
t:4得t=![]()

 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案