Question

【题目】如图，平行四边形ABCD的顶点A，B，D的坐标分别是（0，0）、（5，0）、（2，3），则顶点C的坐标是 ．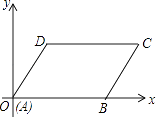

Answer 1

【答案】（7，3）
【解析】解：过点D作DE⊥OB于点E，过点C作CF⊥OB于点F， ∴∠OED=∠BFC=90°，
∵平行四边形ABCD的顶点A，B，D的坐标分别是（0，0）、（5，0）、（2，3），
∴OB∥CD，OD∥BC，
∴DE=CF=3，∠DOE=∠CBF，
在△ODE和△CBF中，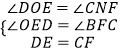
，
∴△ODE≌△CBF（AAS），
∴BF=OE=2，
∴OF=OB+BF=7，
∴点C的坐标为：（7，3）．
故答案为：（7，3）．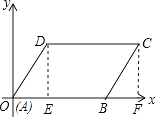

首先过点D作DE⊥OB于点E，过点C作CF⊥OB于点F，易证得△ODE≌△CBF，则可得CF=DE=3，BF=OE=2，继而求得OF的长，则可求得顶点C的坐标．