题目内容
【题目】综合题。
(1)化简:2a(a+b)﹣(a+b)2
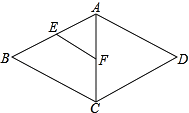
(2)如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.试判断四边形OCED的形状,并说明理由. 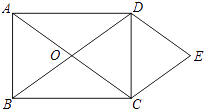
【答案】
(1)解:2a(a+b)﹣(a+b)2,
=(a+b)(2a﹣a﹣b),
=(a+b)(a﹣b),
=a2﹣b2
(2)解:四边形OCED菱形.
理由如下:∵四边形ABCD是矩形,
∴AC=BD,OD= ![]() BD,OC=
BD,OC= ![]() AC,
AC,
∴OC=OD,
∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形,
∴四边形OCED是菱形
【解析】(1)提取公因式(a+b),然后整理即可得解;(2)根据矩形的对角线互相垂直平分求出OC=OD,然后求出四边形OCED是平行四边形,再根据一组邻边相等的平行四边形是菱形证明.
【考点精析】本题主要考查了菱形的判定方法和矩形的性质的相关知识点,需要掌握任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形;矩形的四个角都是直角,矩形的对角线相等才能正确解答此题.

练习册系列答案
 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目