题目内容
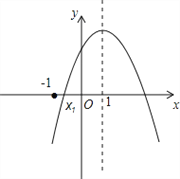
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与![]() 轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:
轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:
① 4ac<b2;② 方程ax2+bx+c=0的两个根是![]() ;③ 3a+c>0;④ 当y>0时,x的取值范围是-1≤x<3;⑤ 当x<0时,y随x增大而增大;
;③ 3a+c>0;④ 当y>0时,x的取值范围是-1≤x<3;⑤ 当x<0时,y随x增大而增大;
其中结论正确有__________.

【答案】①②⑤
【解析】试题解析:∵抛物线与x轴有2个交点,
∴b2-4ac>0,所以①正确;
∵抛物线的对称轴为直线x=1,
而点(-1,0)关于直线x=1的对称点的坐标为(3,0),
∴方程ax2+bx+c=0的两个根是x1=-1,x2=3,所以②正确;
∵x=-![]() =1,即b=-2a,
=1,即b=-2a,
而x=-1时,y=0,即a-b+c=0,
∴a+2a+c=0,所以③错误;
∵抛物线与x轴的两点坐标为(-1,0),(3,0),
∴当-1<x<3时,y>0,所以④错误;
∵抛物线的对称轴为直线x=1,
∴当x<1时,y随x增大而增大,所以⑤正确.
故答案为:①②⑤

练习册系列答案
相关题目
【题目】某校七年级1班体育委员统计了全班同学60秒跳绳的次数,并绘制出如下频数分布表和频数分布直方图:
次数 | 80≤x<100 | 100≤x<120 | 120≤x<140 | 140≤x<160 | 160≤x<180 | 180≤x<200 |
频数 | a | 4 | 12 | 16 | 8 | 3 |
结合图表完成下列问题:
(1)a= ;
(2)补全频数分布直方图;
(3)写出全班人数是 ,并求出第三组“120≤x<140”的频率(精确到0.01)
(4)若跳绳次数不少于140的学生成绩为优秀,则优秀学生人数占全班总人数的百分之几?