Question

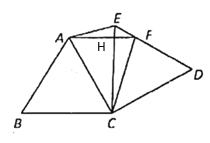
【题目】如图，将等边△ABC绕点C顺时针旋转90得到△DEC，∠ACD的平分线CF交DE于点F，连接AE,AF.

（1）求∠CEA度数；

（2）求证AF⊥CE.

Answer 1

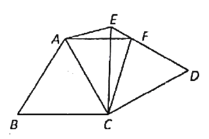
【答案】（1）75°；（2）详见解析.

【解析】

（1）由等边△ABC绕点C顺时针旋转90得到△DEC，得到∠BCE=90，∠ACB=60，CE=AC，

求出∠ACE =30，再根据等边对等角及三角形的内角和即可得到答案；

（2）根据CF平分∠ACD，利用SAS证明△ACF≌△DCF，得到∠CAF=∠D=60，再利用三角形内角和得到∠AHC =90.

（1）∵等边△ABC绕点C顺时针旋转90得到△DEC，

∴∠BCE=90，∠ACB=60，BC=CE=AC=CD,

∴∠ACE=∠BCE-∠ACB=30，

∵∠ACE+∠CEA+∠CAE=,∠CEA=∠CAE,

∴∠CEA=

（2）∵等边△ABC绕点C顺时针旋转90得到△DEC，

∴△DEC是等边三角形，

∴∠D=60，

∵CF平分∠ACD，

∴∠ACF=∠DCF,

又∵AC=CD,CF=CF,

∴△ACF≌△DCF,

∴∠CAF=∠D=60，

设AF交CE于H，

∵∠ACE =30，

∴∠AHC=-∠ACE-∠CAF=90,

∴AF⊥CE.