题目内容
【题目】某养猪场对猪舍进行喷药消毒.在消毒的过程中,先经过![]() 的药物集中喷洒,再封闭猪舍
的药物集中喷洒,再封闭猪舍![]() ,然后再打开窗户进行通风.已知室内每立方米空气中含药量
,然后再打开窗户进行通风.已知室内每立方米空气中含药量![]() (
(![]() )与药物在空气中的持续时间
)与药物在空气中的持续时间![]() (
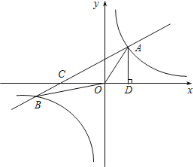
(![]() )之间的函数图象如图所示,其中在打开窗户通风前
)之间的函数图象如图所示,其中在打开窗户通风前![]() 与
与![]() 分别满足两个一次函数,在通风后
分别满足两个一次函数,在通风后![]() 与
与![]() 满足反比例函数.
满足反比例函数.
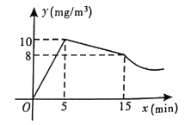
(1)求反比例函数的关系式;
(2)当猪舍内空气中含药量不低于![]() 且持续时间不少于
且持续时间不少于![]() ,才能有效杀死病毒,问此次消毒是否有效?
,才能有效杀死病毒,问此次消毒是否有效?
【答案】(1)![]() ;(2)此次消毒能有效杀死该病毒.
;(2)此次消毒能有效杀死该病毒.
【解析】
(1)用待定系数法求函数解析式;
(2)求正比例函数解析式,计算正比例函数和反比例函数的函数值为5对应的自变量的值,则它们的差为含药量不低于5mg/m3的持续时间,然后与21比较大小即可判断此次消毒是否有效.
解:(1)设反比例函数关系式为![]() .
.
∵反比例函数的图像过点![]() ,
,
∴![]() .
.
∴![]() .
.
(2)设正比例函数关系式为![]() .
.
把![]() ,
,![]() 代入上式,得
代入上式,得![]() .
.
∴![]() .
.
当![]() 时,
时,![]() .
.
把![]() 代入
代入![]() ,得
,得![]() .
.
∴![]() .
.
答:此次消毒能有效杀死该病毒.


练习册系列答案
相关题目
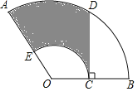
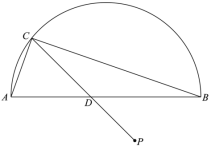
【题目】如图,![]() 是半圆的直径,P是半圆与直径
是半圆的直径,P是半圆与直径![]() 所围成的图形的外部的一定点,D是直径
所围成的图形的外部的一定点,D是直径![]() 上一动点,连接
上一动点,连接![]() 并延长,交半圆于点C,连接
并延长,交半圆于点C,连接![]() .已知
.已知![]() ,设
,设![]() 两点间的距离为
两点间的距离为![]() ,
,![]() 两点之间的距离为
两点之间的距离为![]() 两点之间的距离为
两点之间的距离为![]() .
.
小明根据学习函数的经验,分别对函数![]() 随自变量x的变化而变化的规律进行了探究.
随自变量x的变化而变化的规律进行了探究.
下面是小明的探究过程,请补充完整:
(1)按照下表自变量x的值进行取点、画图、测量,分别得到![]() 与x的几组对应值;
与x的几组对应值;
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 0.47 | 1.31 | 5.02 | 5.91 | 6 | |
| 6 | 5.98 | 5.86 | 5.26 | 3.29 | 1.06 | 0 |
(2)在同一平面直角坐标系![]() 中,描出补全后的表中各组数值所对应的点
中,描出补全后的表中各组数值所对应的点![]() ,
,![]() ,并画出函数
,并画出函数![]() 的图象;
的图象;
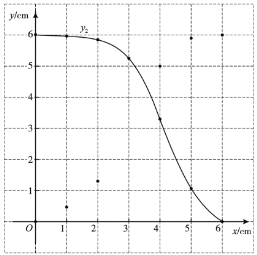
(3)结合函数图象,解决问题:当![]() 有一个角的正弦值为
有一个角的正弦值为![]() 时,
时,![]() 的长约为_____cm.
的长约为_____cm.