Question

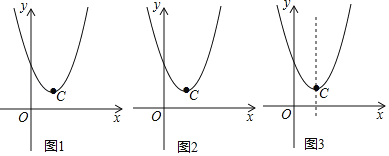
【题目】（1）抛物线y＝ax2﹣2x+2经过点E（2，2），其顶点为C点．

①求抛物线的解析式，并直接写出C点坐标；

②将直线y＝x沿y轴向上平移b（b＞0）个单位长度交抛物线于A、B两点，若∠ACB＝90°，求b的值．

（2）是否存在点D（1，m），使抛物线y＝x2﹣x+上任意一点P到x轴的距离等于P点到点D的距离，若存在，请求点D的坐标，若不存在，请说明理由．

Answer 1

【答案】（1）①y＝x2﹣2x+2， C（1，1）；②b＝1；（2存在，D（1，2）

【解析】

（1）①将点E坐标代入解析式可求解；

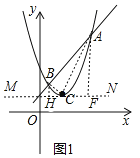
②如图1，过点C作MN⊥y轴，过点A作AF⊥MN，过点B作BH⊥MN，设平移后直线解析式为：y＝x+b，由根与系数关系可得xA+xB＝3，xAxB＝2﹣b，通过证明△ACF∽△CBH，可得，可求b的值；

（2）设P（a，b），由题意可得b＝PD，由两点距离公式可求解．

（1）①∵抛物线y＝ax2﹣2x+2经过点E（2，2），

∴2＝4a﹣4+2，

∴a＝1，

∴抛物线解析式为：y＝x2﹣2x+2，

∵y＝x2﹣2x+2＝（x﹣1）2+1，

∴顶点坐标为（1，1）；

②如图1，过点C作MN⊥y轴，过点A作AF⊥MN，过点B作BH⊥MN，

设平移后直线解析式为：y＝x+b，

∴，

∴x2﹣3x+2﹣b＝0，

设A（xA，yA），B（xB，yB），则xA+xB＝3，xAxB＝2﹣b，

∵∠ACB＝90°，

∴∠BCH+∠ACF＝90°，且∠BCH+∠HBC＝90°，

∴∠HBC＝∠ACF，且∠BHC＝∠AFC＝90°，

∴△ACF∽△CBH，

∴，

∴，

∴yAyB+xAxB+2＝yA+yB+xA+xB，

∴（xA+b）（xB+b）+2﹣b+2＝xA+b+xB+b+3，

∴b2﹣b＝0，

∴b＝1，b＝0（舍去）

（2）设P（a，b），则b＝a2﹣a+，

由题可知，b＝PD，

∴b2＝（a﹣1）2+（m﹣b）2，

∴（4﹣2m）b+m2﹣4＝0，

∵任意一点P，

∴4﹣2m＝0，

∴m＝2，

∴D（1，2）．