题目内容
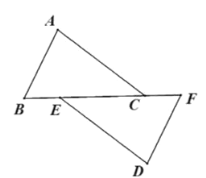
【题目】如图,在△ABC中,∠BAC=110°,点E、G分别是AB、AC的中点,DE⊥AB交BC于D,FG⊥AC交BC于F,连接AD、AF.试求∠DAF的度数.

【答案】40°.
【解析】
先利用三角形内角和得∠B+∠C=70°,然后根据垂直平分线和等腰三角形的性质得到∠BAD=∠B、∠CAF=∠C,最后再利用角的和差即可完成解答.
在△ABC中,∵∠BAC=110°,
∴∠B+∠C=180°﹣110°=70°,
∵E、G分别是AB、AC的中点,
又∵DE⊥AB,FG⊥AC,
∴AD=BD,AF=CF,
∴∠BAD=∠B,∠CAF=∠C,
∴∠DAF=∠BAC﹣(∠BAD+∠CAF)
=∠BAC﹣(∠B+∠C)=110°﹣70°=40°.

练习册系列答案
相关题目