题目内容
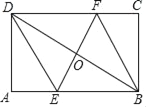
【题目】如图,![]() 为
为![]() 中的一条射线,点
中的一条射线,点![]() 在边
在边![]() 上,
上,![]() 于
于![]() ,交
,交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.

![]() 求证:四边形
求证:四边形![]() 为矩形;
为矩形;
![]() 若
若![]() ,试探究
,试探究![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
【答案】(1)详见解析;(2)![]() ,理由详见解析.
,理由详见解析.
【解析】
(1)根据垂直于同一直线的两直线平行可得PH∥MD,再根据平行于同一直线的两直线平行可得PM∥QR,然后求出四边形PQRM是平行四边形,再求出∠MPQ=90°,根据有一个角是直角的平行四边形是矩形证明即可;
(2)根据矩形的对角线互相平分可得PS=![]() PR,然后求出OP=PS,根据等边对等角的性质可得∠POS=∠PSO,再根据两直线平行,同位角相等可得∠SQR=∠BON,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠PSO=2∠SQR,然后整理即可得解.
PR,然后求出OP=PS,根据等边对等角的性质可得∠POS=∠PSO,再根据两直线平行,同位角相等可得∠SQR=∠BON,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠PSO=2∠SQR,然后整理即可得解.
![]() ∵
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴四边形![]() 为矩形;
为矩形;
![]() .理由如下:
.理由如下:
∵四边形![]() 为矩形,
为矩形,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() .
.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目