题目内容
【题目】已知△ABC中,BC=6,AB、AC的垂直平分线分别交边BC于点M、N,若MN=2,则△AMN的周长是_____.
【答案】6或10
【解析】
由直线PM为线段AB的垂直平分线,根据线段垂直平分线定理:线段垂直平分线上的点到线段两端点的距离相等可得AM=BM,同理可得AN=NC,然后表示出三角形AMN的三边之和,等量代换可得其周长等于BC的长,由BC的长即可得到三角形AMN的周长.
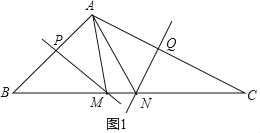
如图1,∵直线MP为线段AB的垂直平分线,
∴MA=MB,
又直线NQ为线段AC的垂直平分线,
∴NA=NC,
∴△AMN的周长l=AM+MN+AN=BM+MN+NC=BC,
又BC=6,
则△AMN的周长为6;
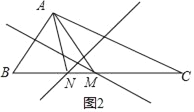
如图2,△AMN的周长l=AM+MN+AN=BM+MN+NC=BC+2MN,
又BC=6,
则△AMN的周长为10,
故答案为:6或10.

练习册系列答案
相关题目