题目内容
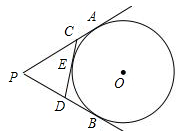
如图,PA、PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C、D,若⊙O的半径为r,△PCD的周长等于3r,则tan∠APB的值是( )
A.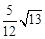 B.
B.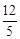 C.
C.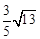 D.
D.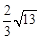

A.
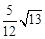 B.
B.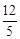 C.
C.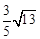 D.
D.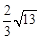
B.
试题分析:如答图,连接PO,AO,取AO中点G,连接AG,过点A作AH⊥PO于点H,
∵PA、PB切⊙O于A、B两点,CD切⊙O于点E,
∴PA=PB,CA=CE,DB=DE,∠APO=∠BPO,∠OAP=90º.
∵△PCD的周长等于3r,∴PA=PB=
 .
.∵⊙O的半径为r,∴在Rt△APO中,由勾股定理得
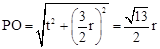 . ∴
. ∴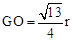 .
.∵∠OHA=∠OAP=90º, ∠HOA=∠AOP,∴△HOA∽△AOP. ∴
 ,即
,即 .
.∴
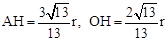 .∴
.∴ .
.∵∠AGH=2∠APO=∠APB, ∴
 .
.故选B.


练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
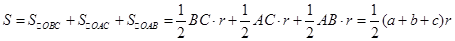 .
.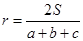 .
.
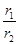 的值.
的值.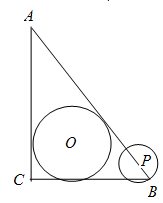


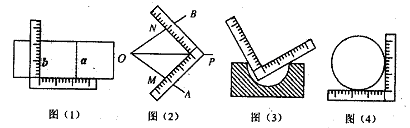
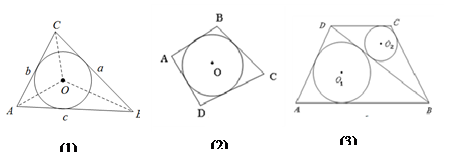
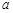 与b,如图⑴;②可以画出∠AOB的平分线OP,如图⑵所示;③可以检验工件的凹面是否为半圆,如图⑶所示;④可以量出一个圆的半径,如图⑷所示.这四种说法正确的个数有 ( )
与b,如图⑴;②可以画出∠AOB的平分线OP,如图⑵所示;③可以检验工件的凹面是否为半圆,如图⑶所示;④可以量出一个圆的半径,如图⑷所示.这四种说法正确的个数有 ( )