��Ŀ����
����Ŀ���Ķ����в��ϣ�Ȼ�������⣮
�������ı���(��������)�������Բ����������ı��ε����Բ��Բ�������ı��εĶԳ����ģ�������ı��ν������Բ���ڽ����ı�����
��ͼ��������ABCD�ڽ��ڡ�O����O�����ΪS1��������ABCD�����ΪS2����Բ��OΪ��������MON��ʹ��MON��90��������MON�Ƶ�O��ת��OM��ON�ֱ����O���ڵ�E��F���ֱ���������ABCD�ı߽��ڵ�G��H������OE��OF��![]() ��������ABCD�ı�Χ�ɵ�ͼ��(��Ӱ����)�����ΪS��
��������ABCD�ı�Χ�ɵ�ͼ��(��Ӱ����)�����ΪS��
��1����OM������Aʱ(��ͼ��)����S��S1��S2֮��Ĺ�ϵΪ�� (�ú�S1��S2�Ĵ���ʽ��ʾ)��
��2����OM��AB��Gʱ(��ͼ��)����(1)�еĽ�����Ȼ��������˵�����ɣ�
��3������MON��ת������λ��ʱ����ͼ�ۣ�����1���еĽ�����Ȼ��������˵������.

���𰸡���1��![]() ��
��
��2����1���еĽ�����Ȼ���������ɼ�������
��2����1���еĽ�����Ȼ���������ɼ�����.
�������������������1����������ε����ʼ�����ֱ�������ε����ʣ����ó����ۣ�
��2����Ȼ��������֤���ı���OGHBΪ�����Σ���������Ӱ���ֵ����Ϊ����OEF�������ȥ������OGBH�������
��3����Ȼ��������O��OR��AB��OS��BC������ֱ�ΪR��S�����֤����ORG�ա�OSH���ɵó��ı���ORBS�����=�ı���OGBH�����������������OEF�������������ORBS��������ɵó����ۣ�
�����������1����OM������Aʱ�������ε����ʿ�֪����MON=90����
��S��OAB=![]() S������ABCD=
S������ABCD=![]() S2��S����OEF=
S2��S����OEF=![]() SԲO=
SԲO=![]() S1��
S1��
��S=S����OEF-S��OAB=![]() SԲO-
SԲO-![]() S������ABCD=
S������ABCD=![]() S1-
S1-![]() S2=
S2=![]() ��S1-S2����
��S1-S2����
��2��������Ȼ�������������£�
�ߡ�EOF=90����
��S����OEF=![]() SԲO=
SԲO=![]() S1
S1
�ߡ�OGB=��EOF=��ABC=90����
���ı���OGBHΪ���Σ�
��OM��AB��
��BG=![]() AB=
AB=![]() BC=BH��
BC=BH��
���ı���OGBHΪ�����Σ�
��S�ı���OGBH=BG2=��![]() AB��2=
AB��2=![]() S2��
S2��
��S=S����OEF-S�ı���OGBH=![]() S1-
S1-![]() S2=
S2=![]() ��S1-S2����
��S1-S2����
��3����1���еĽ�����Ȼ�������������£�
�ߡ�EOF=90����
��S����OEF=![]() SԲO=
SԲO=![]() ��
��
��O��OR��AB��OS��BC������ֱ�ΪR��S��
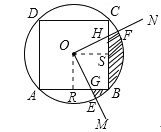
�ɣ�2����֪�ı���ORBSΪ�����Σ�
��OR=OS��
�ߡ�ROS=90������MON=90����
���ROG=��SOH=90��-��GOS��
����ROG����SOH��
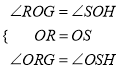 ��
��
���ROG�ա�SOH��ASA����
��S��ORG=S��OSH��
��S�ı���OGBH=S������ORBS��
�ɣ�2����֪S������ORBS=![]() S2��
S2��
��S�ı���OGBH=![]() S2��
S2��
��S=S����OEF-S�ı���OGBH=![]() ��S1-S2����
��S1-S2����

 �������ϵ�д�
�������ϵ�д�
