题目内容
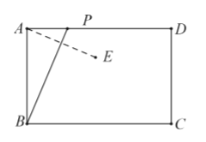
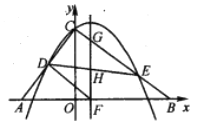
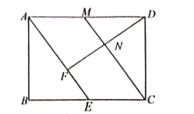
【题目】如图，在矩形
中，点E为
的中点，连接
，过点D作
于点F，过点C作
于点N，延长
交
于点M．
（1）求证：
（2）连接CF，并延长CF交AB于G
①若
，求
的长度；
②探究当
为何值时，点G恰好为AB的中点．
【答案】（1）证明见解析；（2） ①2；②当
时，点G恰好为AB中点．
【解析】
（1）证出四边形
是平行四边形，得出
，由中点的定义得出
，得出
，即可得出结论；
（2）①连接
，由平行四边形性质得出
，证出
，由线段垂直平分线的性质得出
，由矩形的性质得出
；
②设
，
，则
，由勾股定理得出
，作
交
于
，由相似三角形的性质得出
，得出
，证明
，得出
，得出
，即可得出结论．
（1）证明：
，
，
，
四边形
是矩形，
，
，
四边形是平行四边形，
，
点
为
的中点，
，
，
；
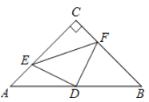
（2）解：①连接，如图1所示：
四边形是平行四边形，
，
，
，
，
，
，
垂直平分线段
，
，
，四边形是矩形，
；
②设，，
则，
，
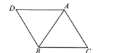
作交于，如图2所示：
当
为
中点时，
，
，
，
，
，
，
，
，即
，
整理得：
，
解得：
（负值舍去），
，
，
即当时，点恰为的中点．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
