题目内容
 如图△ABC与△BDE都是正三角形,且AB<BD,若△ABC不动,将△BDE绕B点旋转,则在旋转过程中,AE与CD的大小关系是( )
如图△ABC与△BDE都是正三角形,且AB<BD,若△ABC不动,将△BDE绕B点旋转,则在旋转过程中,AE与CD的大小关系是( )| A、AE=CD | B、AE>CD |
| C、AE<CD | D、无法确定 |
考点:旋转的性质,全等三角形的判定与性质
专题:
分析:首先猜测AE=CD,那么就应证明AE和CD所在的三角形全等.当有两个等边三角形如此排列的时候,可得△CBD≌△ABE,得到一组对应角相等,进而求得△CBD≌△ABE即可得证.
解答:解:∵△ABC与△BDE都是正三角形,
∴AB=BC,BD=BE,∠ABC=∠DBE,
∴∠ABC+∠ABD=∠DBE+∠ABD,
∴∠CBD=∠ABE,
在△CBD和△ABE中
∴△CBD≌△ABE(SAS),
∴AE=CD,
故选A.
∴AB=BC,BD=BE,∠ABC=∠DBE,
∴∠ABC+∠ABD=∠DBE+∠ABD,
∴∠CBD=∠ABE,
在△CBD和△ABE中
|
∴△CBD≌△ABE(SAS),
∴AE=CD,
故选A.
点评:本题考查了全等三角形的判定与性质及等边三角形的性质;简单的线段相等,可以通过全等三角形来证明,要判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.

练习册系列答案
相关题目
 如图,⊙O是△ABC的外接圆,若∠AOB=100°,则∠ACB的度数是( )
如图,⊙O是△ABC的外接圆,若∠AOB=100°,则∠ACB的度数是( )| A、40° | B、50° |
| C、60° | D、80° |
 如图,为了估算河的宽度,小明采用的办法是:在河的对岸选取一点A,在近岸取点D,B,使得A,D,B在一条直线上,且与河的边沿垂直,测得BD=10m,然后又在垂直AB的直线上取点C,并量得BC=30m.如果DE=20m,则河宽AD为( )
如图,为了估算河的宽度,小明采用的办法是:在河的对岸选取一点A,在近岸取点D,B,使得A,D,B在一条直线上,且与河的边沿垂直,测得BD=10m,然后又在垂直AB的直线上取点C,并量得BC=30m.如果DE=20m,则河宽AD为( )| A、20m | ||
B、
| ||
| C、10m | ||
| D、30m |
下面在平面直角坐标系中所给的四个图象中,是函数图象的是( )
A、 |
B、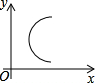 |
C、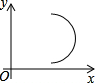 |
D、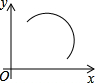 |
 如图,在两个同心圆中,四条直径把大圆分成八等份,若往圆面投掷飞镖,则飞镖落在黑色区域的概率是( )
如图,在两个同心圆中,四条直径把大圆分成八等份,若往圆面投掷飞镖,则飞镖落在黑色区域的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
 已知AB=AD,∠BAD=∠CAE,请添加一个条件
已知AB=AD,∠BAD=∠CAE,请添加一个条件