题目内容
已知:二次函数y=x2+bx-3的图象经过点A(2,5).
(1)求二次函数的解析式;
(2)求二次函数的图象与x轴的交点坐标;
(3)将(1)中求得的函数解析式用配方法化成y=(x-h)2+k的形式.
(1)求二次函数的解析式;
(2)求二次函数的图象与x轴的交点坐标;
(3)将(1)中求得的函数解析式用配方法化成y=(x-h)2+k的形式.
考点:待定系数法求二次函数解析式,二次函数的三种形式,抛物线与x轴的交点
专题:计算题
分析:(1)直接把A点坐标代入y=x2+bx-3可求出b,从而确定二次函数的解析式;
(2)根据抛物线与x轴的交点解方程x2+2x-3=0,即可得到二次函数的图象与x轴的交点坐标;
(3)利用配方法求解.
(2)根据抛物线与x轴的交点解方程x2+2x-3=0,即可得到二次函数的图象与x轴的交点坐标;
(3)利用配方法求解.
解答:解:(1)∵二次函的图象经过点A(2,5),
∴4a+2b-3=5,解得b=2,
∴二次函数的解析式为y=x2+2x-3;
(2)令y=0,则x2+2x-3=0,解得x1=-3,x2=1,
∴二次函数的图象与x轴的交点坐标为(-3,0)和(1,0);
(3)y=x2+2x-3
=(x+1)2-4.
∴4a+2b-3=5,解得b=2,
∴二次函数的解析式为y=x2+2x-3;
(2)令y=0,则x2+2x-3=0,解得x1=-3,x2=1,
∴二次函数的图象与x轴的交点坐标为(-3,0)和(1,0);
(3)y=x2+2x-3
=(x+1)2-4.
点评:本题考查了用待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
下列图案由正多边形拼成,其中是轴对称图形的有( )


| A、1个 | B、2个 | C、3个 | D、4个 |
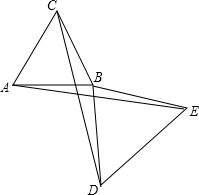 如图△ABC与△BDE都是正三角形,且AB<BD,若△ABC不动,将△BDE绕B点旋转,则在旋转过程中,AE与CD的大小关系是( )
如图△ABC与△BDE都是正三角形,且AB<BD,若△ABC不动,将△BDE绕B点旋转,则在旋转过程中,AE与CD的大小关系是( )| A、AE=CD | B、AE>CD |
| C、AE<CD | D、无法确定 |
 如图,AB为⊙O的直径,点C在⊙O 上,点P是直径AB上的一点,(不与A,B重合),过点P作AB的垂线交BC的延长线于点Q.
如图,AB为⊙O的直径,点C在⊙O 上,点P是直径AB上的一点,(不与A,B重合),过点P作AB的垂线交BC的延长线于点Q.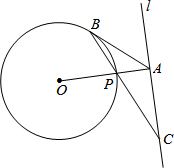 如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,点B是⊙O 上一点,连接BP并延长,交直线l于点C,使得AB=AC.
如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,点B是⊙O 上一点,连接BP并延长,交直线l于点C,使得AB=AC.