��Ŀ����
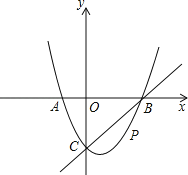
����Ŀ����ͼ����ƽ��ֱ������ϵ�У����κ���y��x2+bx+c��ͼ����x�ύ��A��B���㣬A����ԭ�����࣬B�������Ϊ��3��0������y�ύ��C��0����3���㣬��P��ֱ��BC�·�����������һ���㣮
��1���ֱ����ͼ��ֱ�ߺ������ߵĺ�������ʽ��
��2������PO��PC�����ѡ�POC��C O���ۣ��õ��ı���POP��C����ô�Ƿ���ڵ�P��ʹ�ı���POP��CΪ���Σ������ڣ��������ʱ��P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y��x��3��y��x2��2x��3����2�����ڣ���P
��������
��1����һ�κ�������ʽΪ��y=mx+n����B��C������ֱ����һ�κ�������ʽ�Ͷ��κ�������ʽ���ɽ����
��2�����ı���![]() �����Σ�
�����Σ�![]() ��OC���ֱ��P����������
��OC���ֱ��P����������![]() ��������κ�������ʽ���ɽ�ã�
��������κ�������ʽ���ɽ�ã�
�⣺��1����ֱ��BC�Ľ���ʽΪ��y��mx+n���У�
![]() ��
��
��ã�m��1��n����3��
��ֱ��BC��y��x��3��
����B��C���������y��x2+bx+c�У��ã�
![]() ��
��
��ã�b����2��c����3��
�������ߣ�y��x2��2x��3��
��2���������εĶԽ����ഹֱƽ�֣����Ե�P����OC�Ĵ�ֱƽ�����ϣ����P��������Ϊ��![]() ������������y��x2��2x��3�еã�
������������y��x2��2x��3�еã�
��![]() ��x2��2x��3��
��x2��2x��3��
��� x1��![]() ��x2��
��x2��![]() ����ȥ��
����ȥ��
����P

 ͬ��ѧ��һ�ζ���ϵ�д�
ͬ��ѧ��һ�ζ���ϵ�д� �����ܾ�ϵ�д�
�����ܾ�ϵ�д� ���ƿ�����ϵ�д�
���ƿ�����ϵ�д� ���¿쳵����������ϵ�д�
���¿쳵����������ϵ�д�