题目内容
【题目】完成下列证明过程．
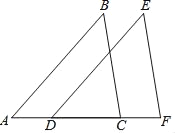
如图，已知AB∥DE，AB＝DE，D，C在AF上，且AD＝CF，求证：△ABC≌△DEF．
证明：∵AB∥DE
∴∠_____＝∠_____（_______）
∵AD＝CF
∴AD+DC＝CF+DC即_____
在△ABC和△DEF中AB＝DE_____
∴△ABC≌△DEF_____．
【答案】∠A ∠EDC 两直线平行，同位角相等 AC＝DF ∠A＝∠EDC，AC＝DF （SAS）
【解析】
根据平行线的性质可得∠A＝∠EDC，根据等式的性质可得AC＝DF，然后利用SAS判定△ABC≌△DEF即可．
∵AB∥DE
∴∠A＝∠EDC（两直线平行，同位角相等）
∵AD＝CF
∴AD+DC＝CF+DC，即AC＝DF．
在△ABC和△DEF中，∵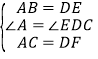
，∴△ABC≌△DEF （SAS）．
练习册系列答案
相关题目
