题目内容
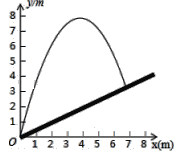
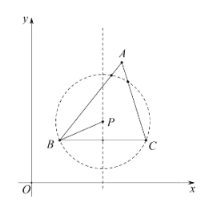
【题目】在平面直角坐标系xoy中,对于已知的△ABC,点P在边BC的垂直平分线上,若以P点为圆心,PB为半径的⊙P与△ABC三条边的公共点个数之和大于等于3,则称点P为△ABC关于边BC的“稳定点”.如图为△ABC关于边BC的一个“稳定点”P的示意图,已知A(m,0),B(0,n).
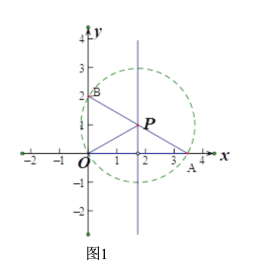
(1) 如图1,当![]() 时,在点
时,在点![]() 中,△AOB关于边OA的“稳定点”是________.
中,△AOB关于边OA的“稳定点”是________.
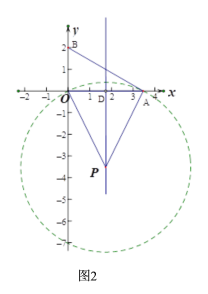
(2) 如图2,当n=4时,若直线y=6上存在△AOB关于边AB的“稳定点”,则m的取值范围是___________
(3)如图3,当m=3,![]() 时,过点M(5,7)的直线y=kx+b上存在△AOB关于边AB的“稳定点”,则k的取值范围是__________________.
时,过点M(5,7)的直线y=kx+b上存在△AOB关于边AB的“稳定点”,则k的取值范围是__________________.

【答案】(1)![]() ;(2)m>
;(2)m>![]() 或m<-
或m<-![]() ;(3)若1≤n<
;(3)若1≤n<![]() 时,
时,![]() <k≤
<k≤![]() ;若
;若![]() 时,
时,![]() ;若
;若![]() <n≤3时,
<n≤3时,![]() ≤k<
≤k<![]() 时,若3<n<
时,若3<n<![]() 时,
时,![]() ≤k<
≤k<![]() ;若n=
;若n=![]() 时,
时,![]() ≤k;若
≤k;若![]() <n≤6时,k<
<n≤6时,k<![]() 或k≥
或k≥![]() .
.
【解析】
(1)分两种情况:①当⊙P过点B时,②当⊙P与直线AB相切时,分别求出点P的坐标,进而得到结论;
(2)分两种情况:①如图3,当点A在x轴的正半轴时,以线段AB的中垂线与直线y=6的交点P为圆心,以PB的长为半径作⊙P,求出A的坐标,②如图4,当点A在x轴的负半轴时,以线段AB的中垂线与直线y=6的交点P为圆心,以PB的长为半径作⊙P,求出A的坐标,进而即可得到结论;
(3)分6种情况:①如图5,若线段AB的中垂线过点M时,即![]() 时,②若1≤n<
时,②若1≤n<![]() 时,如图6,③若
时,如图6,③若![]() <n≤3时,④若3<n<
<n≤3时,④若3<n<![]() 时,⑤若n=
时,⑤若n=![]() 时,⑥若
时,⑥若![]() <n≤6时,分别求出k的求值范围,即可.
<n≤6时,分别求出k的求值范围,即可.
(1)①当⊙P过点B时,如图1,则OP=AP=BP,即:点P是AB的中点,此时,P(![]() ,1),
,1),
②当⊙P与直线AB相切时,如图2,切点为点A,则∠PAB=90°,
∵OA=![]() ,OB=2,∠AOB=90°,
,OB=2,∠AOB=90°,
∴∠BAO=30°,
∴∠OAP=60°,
∴DP=![]() AD=
AD=![]() ×
×![]() =3,
=3,
∴此时,P(![]() ,-3)
,-3)
综上所述,设点P的纵坐标为y,当-3<y≤1时,点P是△AOB关于边OA的“稳定点”,即:![]() 是△AOB关于边OA的“稳定点”.
是△AOB关于边OA的“稳定点”.
故答案是:![]() ;
;
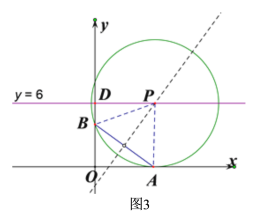
(2)①如图3,当点A在x轴的正半轴时,以线段AB的中垂线与直线y=6的交点P为圆心,以PB的长为半径作⊙P,
当n=4时,且⊙P与x轴相切,切点为点A,则∠PAO=90°,四边形PAOD是矩形,PA=OD=6,
∴PB=PA=6,BD=OD-OB=6-4=2,
∴PD=![]() =
=![]() ,
,
∴此时,A(![]() ,0),
,0),
∴当m>![]() 时,直线y=6上存在△AOB关于边AB的“稳定点”;
时,直线y=6上存在△AOB关于边AB的“稳定点”;
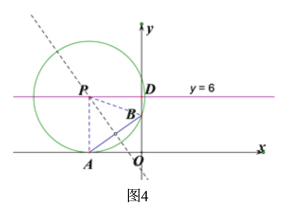
②如图4,当点A在x轴的负半轴时,以线段AB的中垂线与直线y=6的交点P为圆心,以PB的长为半径作⊙P,此时,A(-![]() ,0),
,0),
∴当m<-![]() 时,直线y=6上存在△AOB关于边AB的“稳定点”,
时,直线y=6上存在△AOB关于边AB的“稳定点”,
综上所述,m的取值范围是:m>![]() 或m<-
或m<-![]() .
.
故答案是:m>![]() 或m<-
或m<-![]() ;
;
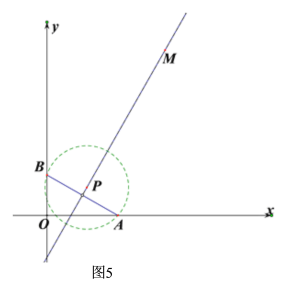
(3)①如图5,若线段AB的中垂线过点M时,即过点M(5,7)的直线y=kx+b与线段AB的中垂线重合,此时,符合条件.
把M(5,7)和AB的中点坐标(![]() ,
,![]() )代入y=kx+b,得
)代入y=kx+b,得 ,解得:
,解得: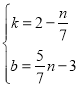 ,
,
设直线AB的解析式为:y=ax+c,则![]() ,解得:
,解得: ,
,
∴(![]() )(
)(![]() )=-1,解得:
)=-1,解得: ![]() ,
,![]() (舍去),
(舍去),
∴![]() ;
;
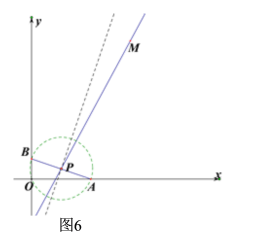
②若1≤n<![]() 时,如图6,当⊙P过点O时,P(
时,如图6,当⊙P过点O时,P(![]() ,
,![]() ),此时,
),此时,![]() ,
,
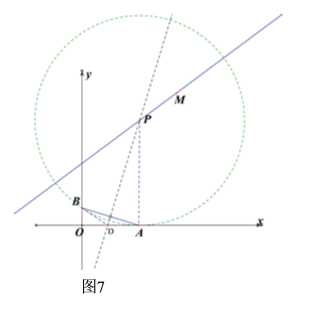
如图7,当⊙P与x轴相切,切点为点A,设OD=x,则AD=BD=3-x,
由勾股定理得:![]() ,解得:
,解得:![]() ,
,
∴AD=3-x=3-![]() =
=![]() ,
,
∵∠APD+∠ADP=∠ADP+∠BAO=90°,
∴∠APD=∠BAO,
∴tan∠APD=tan∠BAO,
∴![]() ,解得:AP=
,解得:AP=![]() ,
,
∴P(3,![]() ),
),
∴k=![]() ,
,
∴![]() <k≤
<k≤![]() 时,过点M(5,7)的直线y=kx+b上存在△AOB关于边AB的“稳定点”;
时,过点M(5,7)的直线y=kx+b上存在△AOB关于边AB的“稳定点”;
③若![]() <n≤3时,当⊙P过点O时,P(
<n≤3时,当⊙P过点O时,P(![]() ,
,![]() ),此时,
),此时,![]() ,
,
当⊙P与x轴相切,切点为点A,此时P(3,![]() ),k=
),k=![]() ,
,
∴![]() ≤k<
≤k<![]() 时,过点M(5,7)的直线y=kx+b上存在△AOB关于边AB的“稳定点”;
时,过点M(5,7)的直线y=kx+b上存在△AOB关于边AB的“稳定点”;
④若3<n<![]() 时,当⊙P过点O时,P(
时,当⊙P过点O时,P(![]() ,
,![]() ),此时,
),此时,![]() ,
,
当⊙P与y轴相切,切点为点B,此时⊙P的半径=![]() ,P(
,P(![]() ,n),k=
,n),k=![]() ,
,
∴![]() ≤k<
≤k<![]() 时,过点M(5,7)的直线y=kx+b上存在△AOB关于边AB的“稳定点”;
时,过点M(5,7)的直线y=kx+b上存在△AOB关于边AB的“稳定点”;
⑤若n=![]() 时,则
时,则![]() ≤k时,过点M(5,7)的直线y=kx+b上存在△AOB关于边AB的“稳定点”;
≤k时,过点M(5,7)的直线y=kx+b上存在△AOB关于边AB的“稳定点”;
⑥若![]() <n≤6时,当⊙P过点O时,P(
<n≤6时,当⊙P过点O时,P(![]() ,
,![]() ),此时,
),此时,![]() ,
,
当⊙P与y轴相切,切点为点B,此时⊙P的半径=![]() ,P(
,P(![]() ,n),k=
,n),k=![]() ,
,
∴k<![]() 或k≥
或k≥![]() 时,过点M(5,7)的直线y=kx+b上存在△AOB关于边AB的“稳定点”;
时,过点M(5,7)的直线y=kx+b上存在△AOB关于边AB的“稳定点”;
综上所述:若1≤n<![]() 时,
时,![]() <k≤
<k≤![]() ;若
;若![]() 时,
时,![]() ;若
;若![]() <n≤3时,
<n≤3时,![]() ≤k<
≤k<![]() 时,若3<n<
时,若3<n<![]() 时,
时,![]() ≤k<
≤k<![]() ;若n=
;若n=![]() 时,
时,![]() ≤k;若
≤k;若![]() <n≤6时,k<
<n≤6时,k<![]() 或k≥
或k≥![]() .
.
故答案是:若1≤n<![]() 时,
时,![]() <k≤
<k≤![]() ;若
;若![]() 时,
时,![]() ;若
;若![]() <n≤3时,
<n≤3时,![]() ≤k<
≤k<![]() 时,若3<n<
时,若3<n<![]() 时,
时,![]() ≤k<
≤k<![]() ;若n=
;若n=![]() 时,
时,![]() ≤k;若
≤k;若![]() <n≤6时,k<
<n≤6时,k<![]() 或k≥
或k≥![]() .
.

 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案【题目】《中国诗词大会》以“赏中华诗词、寻文化基因、品生活之美”为基本宗旨,力求通过对诗词知识的比拼及赏析,带动全民重温那些曾经学过的古诗词,分享诗词之美,感受诗词之趣,从古人的智慧和情怀中汲取营养,涵养心灵,自开播以来深受广大师生的喜爱.某学校为了提高学生的诗词水平,倡导全校3000名学生进行经典诗词诵背活动,并在活动之后举办经典诗词大赛.为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查“一周诗词诵背数量”,根据调查结果绘制成的条形和扇形统计图如图所示.
(整理、描述数据):

大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”:
一周诗词背数量 | 3首 | 4首 | 5首 | 6首 | 7首 | 8首 |
人数 | 16 | 24 | 32 | 78 |
| 35 |
(分析数据):
平均数 | 中位数 | 众数 | |
大赛之前 | 5 |
|
|
大赛之后 | 6 | 6 | 6 |
请根据调查的信息
(1)补全条形统计图;
(2)计算![]() 首,
首,![]() 首,
首,![]() 首,并估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数;
首,并估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数;
(3)根据调査的相关数据,选择适当的统计量评价该校经典诗词诵背系列活动的效果.