题目内容
【题目】如图，在△ABC中，AB=AC，BD=CF，BE=CD，若∠A=40°，则∠EDF的度数为（ ）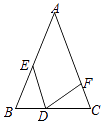 
A.75°
B.70°
C.65°
D.60°
【答案】B
【解析】解：∵AB=AC，∠A=40°∴∠B=∠C=70°
∵EB=BD=DC=CF
∵△BED和△CDF中，
∴△BED≌△CDF（SAS）
∴∠BDE=∠CFD，∠BED=∠CDF
∵∠EDF=180°﹣∠CDF﹣∠BDE=180°﹣（∠CDF+∠BDE）
∵∠B=70°
∴∠BDE+∠BED=110°即∠CDF+∠BDE=110°
∴∠EDF=180°﹣110°=70°．
故选B．
利用等腰三角形的性质及三角形内角和定理先求出∠B、∠C的度数，利用SAS判定△BED≌△CDF，从而得出对应角相等，再利用角与角之间的关系从而求得所求的角．
练习册系列答案
阅读快车系列答案
相关题目
