题目内容
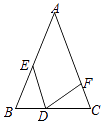
【题目】如图,在Rt△ABC中,∠ACB=90°. 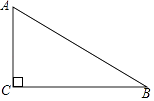
(1)用尺规在边BC上求作一点P,使PA=PB(不写作法,保留作图痕迹);
(2)连结AP,若AC=4,BC=8时,试求点P到AB边的距离.
【答案】
(1)解:如图,点P为所作

(2)解:设BP=x,则AP=x,CP=BC﹣PB=8﹣x,
在Rt△ACP中,
∵PC2+AC2=AP2,
∴(8﹣x)2+42=x2,解得x=5,
即BP的长为5,PC=3,点P到AB的距离为3
【解析】(1)作AB的垂直平分线交BC于P点,则PA=PB;(2)设BP=x,则AP=x,CP=BC﹣PB=8﹣x,然后在Rt△ACP中根据勾股定理得到(8﹣x)2+42=x2 , 再解方程即可.
【考点精析】利用线段垂直平分线的性质和勾股定理的概念对题目进行判断即可得到答案,需要熟知垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

练习册系列答案
相关题目