Question

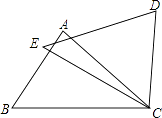
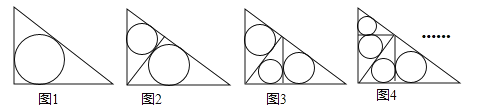
【题目】如图1～4，在直角边分别为3和4的直角三角形中，每多作一条斜边上的高就增加一个三角形的内切圆，依此类推，图10中有10个直角三角形的内切圆，它们的面积分别记为S1，S2，S3，…，S10，则S1+S2+S3+…+S10= ．

Answer 1

【答案】π．

【解析】

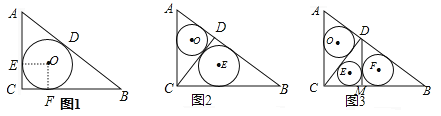
试题分析：（1）图1，过点O做OE⊥AC，OF⊥BC，垂足为E、F，则∠OEC=∠OFC=90°．

∵∠C=90°，∴四边形OECF为矩形．∵OE=OF，∴矩形OECF为正方形．

设圆O的半径为r，则OE=OF=r，AD=AE=3﹣r，BD=4﹣r，∴3﹣r+4﹣r=5，r==1，∴S1==π；

（2）图2，由S△ABC=×3×4=×5×CD，∴CD=．由勾股定理得：AD==，BD=5﹣=．

由（1）得：⊙O的半径==，⊙E的半径==，∴S1+S2==π；

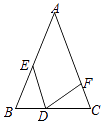
（3）图3，由S△CDB==×4×MD，∴MD=．由勾股定理得：CM==，MB==．由（1）得：⊙O的半径=，：⊙E的半径==，⊙F的半径==，∴S1+S2+S3= =π，∴图4中的S1+S2+S3+S4=π，则S1+S2+S3+…+S10=π．故答案为：π．