题目内容
如图14,矩形ABCD中,AB = 6cm,AD = 3cm,点E在边DC上,且DE = 4cm.动点P从点A开始沿着A→B→C→E的路线以2cm/s的速度移动,动点Q从点A开始沿着AE以1cm/s的速度移动,当点Q移动到点E时,点P停止移动.若点P、Q同时从点A同时出发,设点Q移动时间为t (s),P、Q两点运动路线与线段PQ围成的图形面积为S (cm2),求S与t的函数关系式.
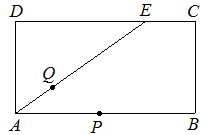

解:在Rt△ADE中,
当0< ≤3时,如图1,过点Q作QM⊥AB于M,连接QP.
≤3时,如图1,过点Q作QM⊥AB于M,连接QP.

∵AB∥CD, ∴∠QAM=∠DEA,
又∵∠AMQ=∠D=90°, ∴△AQM∽△EAD.
∴ ,∴
,∴ .
.

当3< ≤
≤ 时,如图2.
时,如图2.

方法1 :在Rt△ADE 中,
过点Q作QM⊥AB于M, QN⊥BC于N, 连接QB.
∵AB∥CD, ∴∠QAM=∠DEA,
又∵∠AMQ=∠ADE=90°, ∴△AQM∽△EAD.
∴ ,
,  ,
,
∴ .
.
 ,∴QN=
,∴QN= .
.
∴



∴
 +(
+( )
)
方法2 :
过点Q作QM⊥AB于M, QN⊥BC于N,连接QB.
∵AB∥BC, ∴∠QAM=∠DEA,
又∵∠AMQ=∠ADE=90°,∴△AQM∽△EAD.
∴ ,
,  ,
,
∴ .
.
 ,∴QN=
,∴QN= .
.
∴

∴
 +(
+( )
)
当 <
< ≤5时.
≤5时.
方法1 :过点Q作QH⊥CD于H. 如图3.

由题意得QH∥AD,∴△EHQ∽△EDA,∴
∴
∴

∴



方法2:
连接QB、QC,过点Q分别作QH⊥DC于H,QM⊥AB于M,QN⊥BC于N. 如图4.
由题意得QH∥AD,∴△EHQ∽△EDA,∴
∴
∴


∴





当0<
 ≤3时,如图1,过点Q作QM⊥AB于M,连接QP.
≤3时,如图1,过点Q作QM⊥AB于M,连接QP.
∵AB∥CD, ∴∠QAM=∠DEA,
又∵∠AMQ=∠D=90°, ∴△AQM∽△EAD.
∴
 ,∴
,∴ .
.
当3<
 ≤
≤ 时,如图2.
时,如图2. 
方法1 :在Rt△ADE 中,

过点Q作QM⊥AB于M, QN⊥BC于N, 连接QB.
∵AB∥CD, ∴∠QAM=∠DEA,
又∵∠AMQ=∠ADE=90°, ∴△AQM∽△EAD.
∴
 ,
,  ,
,∴
 .
. ,∴QN=
,∴QN= .
.∴




∴

 +(
+( )
)
方法2 :
过点Q作QM⊥AB于M, QN⊥BC于N,连接QB.
∵AB∥BC, ∴∠QAM=∠DEA,
又∵∠AMQ=∠ADE=90°,∴△AQM∽△EAD.
∴
 ,
,  ,
,∴
 .
. ,∴QN=
,∴QN= .
.∴


∴

 +(
+( )
)
当
 <
< ≤5时.
≤5时. 方法1 :过点Q作QH⊥CD于H. 如图3.

由题意得QH∥AD,∴△EHQ∽△EDA,∴

∴

∴


∴




方法2:
连接QB、QC,过点Q分别作QH⊥DC于H,QM⊥AB于M,QN⊥BC于N. 如图4.
由题意得QH∥AD,∴△EHQ∽△EDA,∴

∴

∴



∴





由勾股定理求得AE=5,由于点P可以在AB,BC,CE上,因此分三种情况讨论:
 .
.
 .
.
练习册系列答案
相关题目
 ,与
,与 轴交于A、B两点,点
轴交于A、B两点,点 为抛物线的顶点。点P在抛物线的对称轴上,设⊙P的半径为
为抛物线的顶点。点P在抛物线的对称轴上,设⊙P的半径为 ,当⊙P与
,当⊙P与
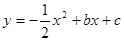 的图象经过A(2,0)B(0,-6)两点
的图象经过A(2,0)B(0,-6)两点
 轴交于点C,连结BA、BC,求△ABC的面积
轴交于点C,连结BA、BC,求△ABC的面积 ,在如图所示的直角坐标系中,求铅球的落点与丁丁的距离.
,在如图所示的直角坐标系中,求铅球的落点与丁丁的距离.
 ,求点B的坐标。
,求点B的坐标。
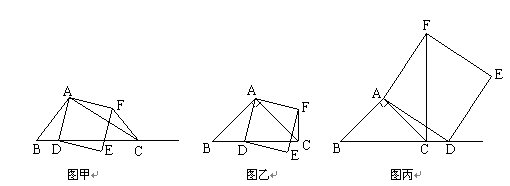
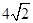 ,BC=3,在(2)的条件下,设正方形ADEF的边DE与线段CF相交于点P,求线段CP长的最大值.
,BC=3,在(2)的条件下,设正方形ADEF的边DE与线段CF相交于点P,求线段CP长的最大值.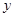 元,镜子的宽是
元,镜子的宽是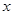 米.
米. 的图像过第一、三、四象限,则函数
的图像过第一、三、四象限,则函数 ( )
( )
