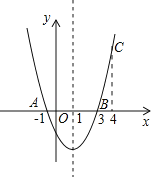题目内容
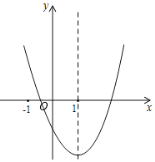
【题目】如图,二次函数y= ax2 + bx +c经过点A(-1,0), B(3,0), C(0,-3).
(1)求该二次函数的解析式.
(2)利用图象的特点填空.
①当x= ___ 时方程ax2 + bx+c=-3.
当x= ___时方程ax2 +bx+c=-4.
②不等式ax2 + bx + c> 0的解集为
不等式-4<ax2+bx+c<0的解集为.
【答案】(1) y=x2-2x-3;(2) ①0或2; 1;②x<-1或x>3;-1<x< 3.
【解析】
(1)将A(-1,0), B(3,0), C(0,-3)三点的坐标分别代入y=ax2+bx+c,然后解方程组即可解决;(2)①令x2-2x-3=-3,解方程即可求出x的解;令x2-2x-3=-4,解方程即可求出x的解;②从题中图象中找出y>0的函数值即可;从题中图象中找出-4<y<0的函数值即可.
(1)解:(1)∵二次函数y=ax2+bx+c的图象经过A(-1,0), B(3,0), C(0,-3)三点,
∴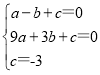 ,解得
,解得![]()
∴二次函数的解析式为:y=x2-2x-3;
(2)①由(1)知y=x2-2x-3
∴x2-2x-3=-3时解得x=0或2
x2-2x-3=-4时解得x=1;
②从题中图象可知y>0时,x的取值为x<-1或x>3
-4<y<0时,x的取值为-1<x< 3.

 阅读快车系列答案
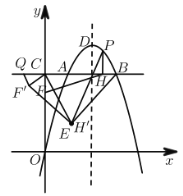
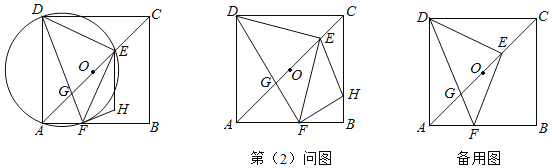
阅读快车系列答案【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() ,
,![]() 为
为![]() 上一动点,过点
上一动点,过点![]() 的直线交
的直线交![]() 于
于![]() 两点,且
两点,且![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,当点
,当点![]() 在
在![]() 上运动时,设
上运动时,设![]() ,
,![]() (当
(当![]() 的值为0或3时,
的值为0或3时,![]() 的值为2),探究函数
的值为2),探究函数![]() 随自变量
随自变量![]() 的变化而变化的规律.
的变化而变化的规律.
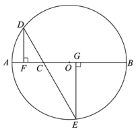
(1)通过取点、画图、测量,得到了x与y的几组对应值,如下表:
| 0 | 0. 40 | 0. 55 | 1. 00 | 1. 80 | 2. 29 | 2. 61 | 3 |
| 2 | 3. 68 | 3. 84 | 3. 65 | 3. 13 | 2. 70 | 2 |
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象,解决问题:点![]() 与点
与点![]() 重合时,
重合时,![]() 长度约为________
长度约为________![]() (结果保留一位小数).
(结果保留一位小数).