题目内容
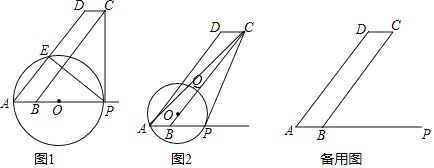
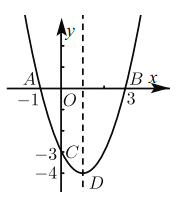
【题目】如图,已知正方形![]() 的边长为2,以点
的边长为2,以点![]() 为圆心,1为半径作圆,
为圆心,1为半径作圆,![]() 是圆
是圆![]() 上的任意一点,将点
上的任意一点,将点![]() 绕点
绕点![]() 按逆时针方向转转
按逆时针方向转转![]() ,得到点
,得到点![]() ,连接
,连接![]() ,则
,则![]() 的最大值是__________.
的最大值是__________.

【答案】![]()
【解析】
先找出AF最大值时,点E的位置,再判断出AF最大时,点C在AF上,根据正方形的性质求出AC,从而得出AF的最大值.
过点A作∠EAB=45°交A于点E,此时旋转后AF最大,
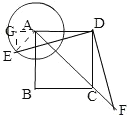
过点E作EG⊥AD交DA延长线于G,
在Rt△AEG中,AE=1,∠GAE=∠EAB=45°,
∴EG=AG=![]() ,
,
∵∠ADC=∠EDF,
∴∠ADE=∠CDF,
在△ADE和△CDF中, 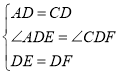 ,
,
∴△ADE≌△CDF,
∴CF=AE=1,
∠DCF=∠DAE=∠BAD+∠EAB=90°+45°=135°
∴点C在线段AF上,
∴AF=AC+CF,
∵AC是边长为2的正方形的对角线,
∴AC=![]() ,
,
∴AF=![]() +1,
+1,
即:AF的最大值是![]() +1,
+1,
故答案为:![]() +1
+1

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目