题目内容
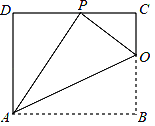
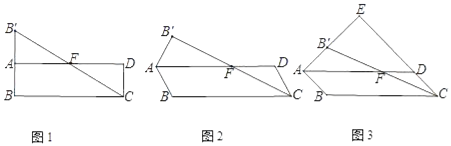
【题目】在ABCD中,点B关于AD的对称点为B′,连接AB′,CB′,CB′交AD于F点.
(1)如图1,∠ABC=90°,求证:F为CB′的中点;
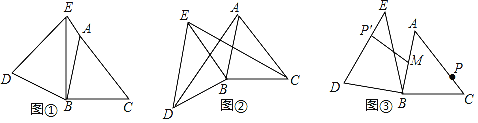
(2)小宇通过观察、实验、提出猜想:如图2,在点B绕点A旋转的过程中,点F始终为CB′的中点.小宇把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:过点B′作B′G∥CD交AD于G点,只需证三角形全等;
想法2:连接BB′交AD于H点,只需证H为BB′的中点;
想法3:连接BB′,BF,只需证∠B′BC=90°.
…
请你参考上面的想法,证明F为CB′的中点.(一种方法即可)
(3)如图3,当∠ABC=135°时,AB′,CD的延长线相交于点E,求![]() 的值.
的值.
【答案】(1)详见解析;(2)详见解析;(3)![]() .
.
【解析】
(1)证明:根据已知条件得到ABCD为矩形,AB=CD,根据矩形的性质得到∠D=∠BAD=90°,根据全等三角形的性质即可得到结论;
(2)方法1:如图2,过点B′作B′G∥CD交AD于点G,由轴对称的性质得到∠1=∠2,AB=AB′,根据平行线的性质得到∠2=∠3,∠1=∠3,根据平行线的性质得到∠4=∠D,根据全等三角形的性质即可得到结论;方法2:连接BB′交直线AD于H点,根据线段垂直平分线的性质得到B′H=HB,由平行线分线段成比例定理得到结论;方法3:连接BB′,BF,根据轴对称的性质得到AD是线段B′B的垂直平分线,根据线段垂直平分线的性质得到B′F=FB,得到∠1=∠2,由平行线的性质得到∠B′BC=90°,根据余角的性质得到∠3=∠4,于是得到结论;
(3)取B′E的中点G,连结GF,由(2)得,F为CB′的中点,根据平行线的性质得到∠BAD=180°-∠ABC=45°,由对称性的性质得到∠EAD=∠BAD=45°,根据平行线的性质得到∠GFA=∠FAB=45°,根据三角函数的定义即可得到结论.
(1)证明:∵四边形ABCD为平行四边形,∠ABC=90°,
∴□ABCD为矩形,AB=CD,
∴∠D=∠BAD=90°,
∵B,B′关于AD对称,
∴∠B′AD=∠BAD=90°,AB=AB′,
∴∠B′AD=∠D,
∵∠AFB′=∠CFD,
在△AFB′与△CFD中,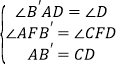 ,
,
∴△AFB′≌△CFD(AAS),
∴FB′=FC,
∴F是CB′的中点;
(2)证明:
方法1:如图2,过点B′作B′G∥CD交AD于点G,
∵B,B′关于AD对称,
∴∠1=∠2,AB=AB′,
∵B′G∥CD,AB∥CD,
∴B′G∥AB.
∴∠2=∠3,
∴∠1=∠3,
∴B′A=B′G,
∵AB=CD,AB=AB′,
∴B′G=CD,
∵B′G∥CD,
∴∠4=∠D,
∵∠B′FG=∠CFD,
在△B′FG与△CFD中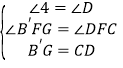 ,
,
∴△B′FG≌△CFD(AAS),
∴FB′=FC,
∴F是CB′的中点;
方法2:连接BB′交直线AD于H点,
∵B,B′关于AD对称,
∴AD是线段B′B的垂直平分线,
∴B′H=HB,
∵AD∥BC,
∴![]() =1,
=1,
∴FB′=FC.
∴F是CB′的中点;
方法3:连接BB′,BF,
∵B,B′关于AD对称,
∴AD是线段B′B的垂直平分线,
∴B′F=FB,
∴∠1=∠2,
∵AD∥BC,
∴B′B⊥BC,
∴∠B′BC=90°,
∴∠1+∠3=90°,∠2+∠4=90°,
∴∠3=∠4,
∴FB=FC,
∴B′F=FB=FC,
∴F是CB′的中点;
(3)解:取B′E的中点G,连结GF,
∵由(2)得,F为CB′的中点,
∴FG∥CE,FG=![]() CE,
CE,
∵∠ABC=135°,□ABCD中,AD∥BC,
∴∠BAD=180°﹣∠ABC=45°,
∴由对称性,∠EAD=∠BAD=45°,
∵FG∥CE,AB∥CD,
∴FG∥AB,
∴∠GFA=∠FAB=45°,
∴∠FGA=90°,GA=GF,
∴FG=sin∠EADAF=![]() AF,
AF,
∴由①,②可得![]() .
.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案