题目内容
【题目】三角形ABC中,∠ABC=105°,过点B作BD⊥AC,垂足为D,E是线段BC上一点,且∠BED=75°,F是射线BA上一点,过点F作FG⊥AC,垂足为G.若∠BDE=55°,则∠BFG=______.
【答案】125°或55°
【解析】
如图,分点F在BA边及BA边延长线上两种情况,根据三角形内角和定理求出∠DBE的度数,再求出∠DBF的度数,根据BD⊥AC,FG⊥AC可证明BD∥FG,利用平行线的性质可得出结论.
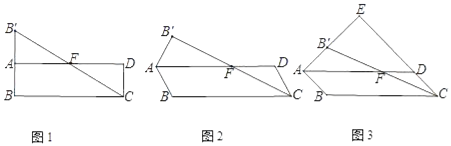
①当点F在BA边上时,如图1,
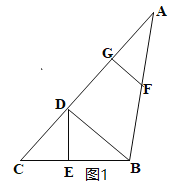
在△BDE中,∠BED=75°,∠BDE=55°,
∴∠DBE=180°-∠BDE-∠BED=180°-55°-75°=50°,
∵∠ABC=105°,
∴∠ABD=105°-50°=55°,
∵BD⊥AC,FG⊥AC,
∴BD∥FG,
∴∠ABD+∠BFG=180°,
∴∠BFG=180°-∠ABD=180°-55°=125°;
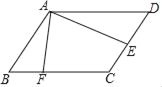
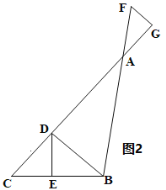
②当点F在BA边延长线上时,如图2,
同①可得∠ABD=55°,BD∥FG,
∴∠BFG=∠ABD=55°,
故答案为:125°或55°.

练习册系列答案
相关题目