题目内容
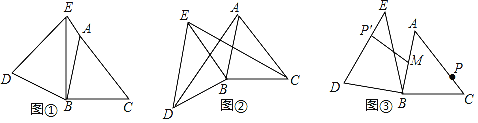
【题目】在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△DBE.
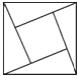
(1)当旋转成如图①,点E在线段CA的延长线上时,则∠CED的度数是 度;
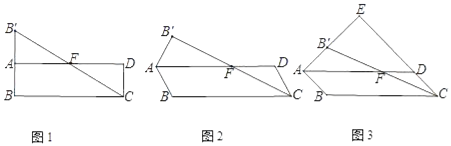
(2)当旋转成如图②,连接AD、CE,若△ABD的面积为4,求△CBE的面积;
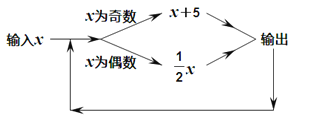
(3)点M为线段AB的中点,点P是线段AC上一动点,在△ABC绕点B按逆时针方向旋转过程中,点P的对应点P′,连接MP′,如图③,直接写出线段MP′长度的最大值和最小值.
【答案】(1)90;(2)S△CBE=![]() ;(3)线段MP'的最大值为7,最小值为
;(3)线段MP'的最大值为7,最小值为![]() ﹣2.
﹣2.
【解析】试题分析:(1)根据旋转的性质可知:∠DEC=45°,再由等边对等角得∠BEC=45°,则∠CED=90°;
(2)由△ABC≌△DBE得出BA=BD,BC=BE,进而得出![]() ,证明△ABD∽△CBE,根据面积比等于相似比的平方求出△CBE的面积;
,证明△ABD∽△CBE,根据面积比等于相似比的平方求出△CBE的面积;
(3)作辅助线,当点P在F处时BP最小,则BG最小,MP'最小;当点P在点C处时,BP最大,则BH最大,MP'最大,代入计算即可得出结论.
试题解析:解:(1)由旋转得:∠DEB=∠ACB=45°,BC=BE,∴∠ACB=∠BEC=45°,∴∠CED=90°.故答案为:90;
(2)∵△ABC≌△DBE,∴BA=BD,BC=BE,∠ABC=∠DBE,∴![]() .∵∠ABD=∠CBE,∴△ABD∽△CBE,∴
.∵∠ABD=∠CBE,∴△ABD∽△CBE,∴![]() =(
=(![]() )2=
)2=![]() .∵S△ABD=4,∴S△CBE=
.∵S△ABD=4,∴S△CBE=![]() ;
;
(3)∵M是AB的中点,∴BM=![]() AB=2.如图③,过点B作BF⊥AC,F为垂足.∵△ABC为锐角三角形,∴点F在线段AC上.在Rt△BCF中,BF=BC×sin45°=
AB=2.如图③,过点B作BF⊥AC,F为垂足.∵△ABC为锐角三角形,∴点F在线段AC上.在Rt△BCF中,BF=BC×sin45°=![]() ,以B为圆心,BF为半径画圆交AB于G,BP'有最小值BG,∴MP'的最小值为MG=BG﹣BM=
,以B为圆心,BF为半径画圆交AB于G,BP'有最小值BG,∴MP'的最小值为MG=BG﹣BM=![]() ﹣2,以B为圆心,BC为半径画圆交AB的延长线于H,BP'有最大值BH.此时MP'的最大值为BM+BH=2+5=7,∴线段MP'的最大值为7,最小值为
﹣2,以B为圆心,BC为半径画圆交AB的延长线于H,BP'有最大值BH.此时MP'的最大值为BM+BH=2+5=7,∴线段MP'的最大值为7,最小值为![]() ﹣2.
﹣2.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案【题目】星光厨具店购进电饭煲和电压锅两种电器进行销售其进价与售价如表
进价(元/台) | 售价(元/台) | |
电饭煲 | 200 | 250 |
电压锅 | 160 | 200 |
(1)一季度,厨具店购进这两种电器共30台,用去了5600元,并且全部售完,问厨具店在该买卖中赚了多少钱?
(2)为了满足市场需求,二季度厨具店决定采购电饭煲和电压锅共50台,且电饭煲的数量不大于电压锅的![]() ,请你通过计算判断,如何进货厨具店赚钱最多?最大利润是多少?
,请你通过计算判断,如何进货厨具店赚钱最多?最大利润是多少?