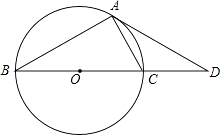Question

【题目】如图1，已知在⊙O中，点C为劣弧AB上的中点，连接AC并延长至D，使CD=CA，连接DB并延长DB交⊙O于点E，连接AE．
（1）求证：AE是⊙O的直径；
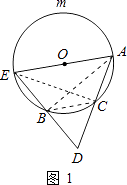
（2）如图2，连接EC，⊙O半径为5，AC的长为4，求阴影部分的面积之和．（结果保留π与根号）

Answer 1

【答案】
（1）证明：连接CB，AB，CE，

∵点C为劣弧AB上的中点，

∴CB=CA，

又∵CD=CA，

∴AC=CD=BC，

∴∠ABC=∠BAC，∠DBC=∠D，

∵Rt△斜边上的中线等于斜边的一半，

∴∠ABD=90°，

∴∠ABE=90°，

即弧AE的度数是180°，

∴AE是⊙O的直径

（2）解：∵AE是⊙O的直径，

∴∠ACE=90°，

∵AE=10，AC=4，

∴根据勾股定理得：CE=2 ，

∴S阴影=S半圆﹣S△ACE=12.5π﹣ ×4×2 =12.5π﹣4

【解析】（1）连接CB，AB，CE，由点C为劣弧AB上的中点，可得出CB=CA，再根据CD=CA，得△ABD为直角三角形，可得出∠ABE为直角，根据90度的圆周角所对的弦为直径，从而证出AE是⊙O的直径；（2）由（1）得△ACE为直角三角形，根据勾股定理得出CE的长，阴影部分的面积等于半圆面积减去三角形ACE的面积．
【考点精析】本题主要考查了勾股定理的概念和圆周角定理的相关知识点，需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能正确解答此题．