题目内容
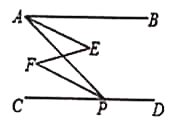
【题目】如图,在正方形![]() 中,点
中,点![]() 是
是![]() 边上的一动点,点
边上的一动点,点![]() 是
是![]() 上一点,且
上一点,且![]() ,
,![]() 、
、![]() 相交于点
相交于点![]() .
.
(1)求证:![]() ;
;
(2)求![]() 的度数
的度数
(3)若![]() ,求
,求![]() 的值.
的值.

【答案】(1)见解析;(2)∠AGD=90°;(3)![]() .
.
【解析】
(1)直接利用正方形的性质得到AD=DC,∠ADF=∠DCE,![]() ,结合全等三角形的判定方法得出答案;
,结合全等三角形的判定方法得出答案;
(2)根据∠DAF=∠CDE和余角的性质可得∠AGD=90°;
(3)利用全等三角形的判定和性质得出△ABH≌△ADG(AAS),即可得出![]() 的值.
的值.
(1)证明:∵四边形ABCD是正方形,
∴AD=DC,∠ADF=∠DCE=90°,
在△ADF和△DCE中
 ;
;
∴△ADF≌△DCE(SAS);
(2)解:由(1)得△ADF≌△DCE,
∴∠DAF=∠CDE,
∵∠ADG+∠CDE=90°,
∴∠ADG+∠DAF=90°,
∴∠AGD=90°,
(3)过点B作BH⊥AG于H
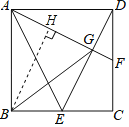
∵BH⊥AG,
∴∠BHA=90°,
∴∠BHA=∠AGD,
∵四边形ABCD是正方形,
∴AB=AD=BC,∠BAD=90°,
∵∠ABH+∠BAH=90°,∠DAG+∠BAH=90°,
∴∠ABH=∠DAG,
在△ABH和△ADG中
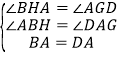 ,
,
∴△ABH≌△ADG(AAS),
∴AH=DG,
∵BG=BC,BA=BC,
∴BA=BG,
∴AH=![]() AG,
AG,
∴DG=![]() AG,
AG,
∴![]() .
.

练习册系列答案
相关题目