题目内容
【题目】如图,AB为⊙O的直径,点C为⊙O上一点,若∠BAC=∠CAM,过点C作直线l垂直于射线AM,垂足为点D.
(1)试判断CD与⊙O的位置关系,并说明理由;
(2)若直线l与AB的延长线相交于点E,⊙O的半径为3,并且∠CAB=30°,求CE的长.

【答案】(1)直线CD与⊙O相切(2)![]()
【解析】解:(1)直线CD与⊙O相切。理由如下:
连接OC,
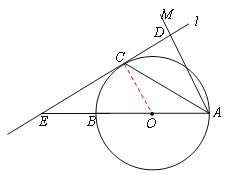
∵OA=OC,∴∠BAC=∠OCA。
∵∠BAC=∠CAM,∴∠OCA=∠CAM。
∴OC∥AM。
∵CD⊥AM ,∴OC⊥CD。
∵OC是⊙O的半径,∴直线CD与⊙O相切。
(2)∵∠CAB=300,∴∠COE=2∠CAB=600。
∴在Rt△COE中,OC=3,CE=OC·tan600=![]() 。
。
(1)要证明过圆上已知点的直线是圆的切线时,只需连接圆心和这点,再证过已知点的半径垂直于这条直线即可。因此,连接CO,根据∠OCA=∠CAM,证明DC∥AD,再根据CD⊥AM,得OC⊥CD,从而证明CD是⊙O的切线。
(2)由题意得∠COE=2∠CAB=600,则在Rt△COE中应用正切函数定义即可求解。.

练习册系列答案
相关题目