Question

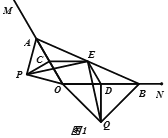
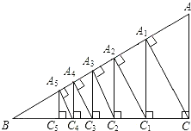
【题目】如图，已知直角三角形ACB，AC=3，BC=4，过直角顶点C作CA1⊥AB，垂足为A1，再过A1作A1C1⊥BC，垂足为C1；过CA1作C1A2⊥AB，垂足为A2，再过A2作A2C2⊥BC，垂足为C2；…，这样一直做下去，得到一组线段A1C1，C2A2，…，则线段AnCn=___.

Answer 1

【答案】3×

【解析】

利用勾股定理求得AB的长,即可得sinA=,在Rt△ACA 中C A= ACsinA=3× ,由∠A+∠AC A=90°、∠C AC+∠ACA=90°得∠A=∠ACC,从而得出AC=CASinA=3 ,同理得出,据此可得出规律

∵Rt△ABC中,AC=3,BC=4

∴AB=

∴ sinA=

∵CA⊥AB

∴在Rt△ACA中,CA= A Csin A=3×,

又∵∠A+∠ACA=90°,∠CAh+∠ACA，

∴∠A=∠ACC，

∴AC=CA. sin A=3，

同理可得，

∴ =3×，

故答案为: 3×