题目内容
【题目】对于平面直角坐标系xOy中的动点P和图形N,给出如下定义:如果Q为图形N上一个动点,P,Q两点间距离的最大值为dmax,P,Q两点间距离的最小值为dmin,我们把dmax+dmin的值叫点P和图形N间的“和距离”,记作d(P,图形N).
(1)如图1,正方形ABCD的中心为点O,A(3,3).
①点O到线段AB的“和距离”d(O,线段AB)=______;
②设该正方形与y轴交于点E和F,点P在线段EF上,d(P,正方形ABCD)=7,求点P的坐标.
(2)如图2,在(1)的条件下,过C,D两点作射线CD,连接AC,点M是射线CD上的一个动点,如果6![]() <d(M,线段AC)<6+3
<d(M,线段AC)<6+3![]() ,直接写出M点横坐标t取值范围.
,直接写出M点横坐标t取值范围.
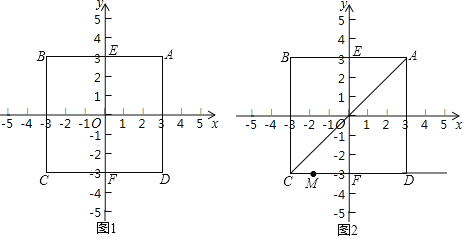
【答案】(1)①![]() ;②点P的坐标为(0,1)或(0,-1);(2)t取值范围是-3<t<3.
;②点P的坐标为(0,1)或(0,-1);(2)t取值范围是-3<t<3.
【解析】
(1)①根据“和距离“的定义计算:OE是两点间距离的最小值,OA是两点间的最大值,相加可得结论;
②分两种情况:P在y轴的正半轴和负半轴上,根据“和距离“的定义,并由d(P,正方形ABCD)=7,列方程计算即可得;
(2)分M在线段CD上和延长线上两种情况,利用“和距离”的定义列方程可得结论.
解:(1)①如图1,连接OA,

∵四边形ABCD是正方形,且A(3,3),
∴dmax+dmin=OE+OA=3+3![]() ,即d(O,线段AB)=3+3
,即d(O,线段AB)=3+3![]() ,
,
故答案为:3+3![]() ;
;
②设P(0,y),
∵d(P,正方形ABCD)=7,
∴dmax+dmin=7,
分两种情况:
∵E(0,3),F(0,-3),且P是线段EF上一个动点,
i)当P在x轴上方时,如图2,连接PC,
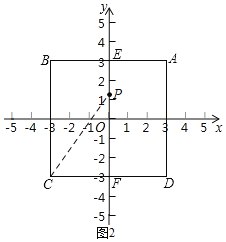
∴dmax+dmin=PE+PC=7,
3-y+![]() =7,
=7,
解得:y=1,
经检验,y=1是原方程的解,
∴P(0,1),
ii)当P在x轴的下方时,同理可得P(0,-1);
综上,点P的坐标为(0,1)或(0,-1);
(2)分两种情况:
①当-3≤t<3时,如图3,M在线段CD上,过M作MN⊥AC于N,连接AM,
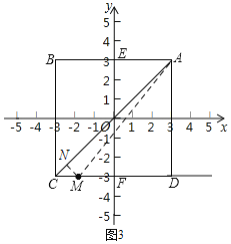
∵M点横坐标是t,
∴CM=t+3,
∵四边形ABCD是正方形,
∴∠ACD=45°,
∴△CMN是等腰直角三角形,
∴MN=![]() (t+3),
(t+3),
∴d(M,线段AC)=MN+MA=![]() (t+3)+
(t+3)+![]() ,
,
②当t≥3时,如图4,M在线段CD的延长线上,过M作MN⊥AC于N,
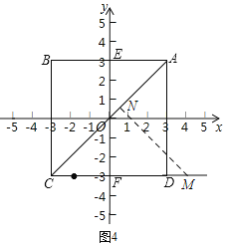
同理MN=![]() =
=![]() (t+3),
(t+3),
∴d(M,线段AC)=MN+CM=![]() (t+3)+t+3,
(t+3)+t+3,
∵在动点M从C到D方向上运动时,MN+MA越来越大,
∴![]() (t+3)+
(t+3)+![]() =6
=6![]() ,解得:t=-3,
,解得:t=-3,
![]() (t+3)+t+3=6+3
(t+3)+t+3=6+3![]() ,解得:t=3,
,解得:t=3,
∴M点横坐标t取值范围是-3<t<3.