题目内容
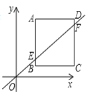
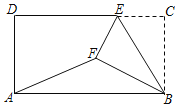
【题目】如图,在矩形ABCD中,AB=4,BC=![]() ,E为CD边上一点,将△BCE沿BE折叠,使得C落到矩形内点F的位置,连接AF,若tan∠BAF=
,E为CD边上一点,将△BCE沿BE折叠,使得C落到矩形内点F的位置,连接AF,若tan∠BAF=![]() ,则CE=_____.
,则CE=_____.
【答案】![]()
【解析】
已知tan∠BAF=![]() ,可作辅助线构造直角三角形,设未知数,利用勾股定理可求出FM、BM,进而求出FN,再利用三角形相似和折叠的性质求出EC.
,可作辅助线构造直角三角形,设未知数,利用勾股定理可求出FM、BM,进而求出FN,再利用三角形相似和折叠的性质求出EC.
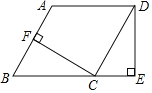
过点F作MN∥AD,交AB、CD分别于点M、N,则MN⊥AB,MN⊥CD,
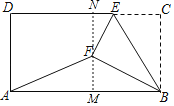
由折叠得:EC=EF,BC=BF=![]() ,∠C=∠BFE=90°,
,∠C=∠BFE=90°,
∵tan∠BAF=![]() =
=![]() ,设FM=x,则AM=2x,BM=4﹣2x,
,设FM=x,则AM=2x,BM=4﹣2x,
在Rt△BFM中,由勾股定理得:
x2+(4﹣2x)2=(![]() )2,
)2,
解得:x1=1,x2=![]() >2舍去,
>2舍去,
∴FM=1,AM=BM=2,
∴FN=![]() ﹣1,
﹣1,
易证△BMF∽△FNE,
∴![]() ,即:
,即:![]() ,
,
解得:EF=![]() =EC.
=EC.
故答案为:![]() .
.

练习册系列答案
相关题目