题目内容
【题目】如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图象与直线
的图象与直线![]() 交于点A(3,m).
交于点A(3,m).
(1)求k、m的值;
(2)已知点P(n,n)(n>0),过点P作平行于![]() 轴的直线,交直线y=x-2于点M,过点P作平行于y轴的直线,交函数
轴的直线,交直线y=x-2于点M,过点P作平行于y轴的直线,交函数![]() 的图象于点N.
的图象于点N.
①当n=1时,判断线段PM与PN的数量关系,并说明理由;
②若PN≥PM,结合函数的图象,直接写出n的取值范围.
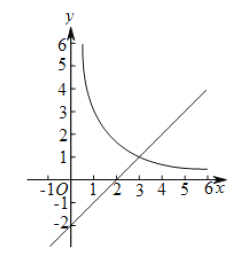
【答案】(1) k的值为3,m的值为1;(2)0<n≤1或n≥3.
【解析】试题分析:(1)先求A 点坐标,在代入![]() ,即可求出结果;(2)①令y=1,求出PM的值,令x=1求出PN的值即可;(3)过点P作平行于x轴的直线,利用图象可得出结果.
,即可求出结果;(2)①令y=1,求出PM的值,令x=1求出PN的值即可;(3)过点P作平行于x轴的直线,利用图象可得出结果.
试题解析:(1) ∵函数![]() (x>0)的图象与直线y=x-2交于点A(3,m) ∴m=3-2=1,把A(3,1)代入
(x>0)的图象与直线y=x-2交于点A(3,m) ∴m=3-2=1,把A(3,1)代入![]() 得,k=3×1=3,即k的值为3,m的值为1;
得,k=3×1=3,即k的值为3,m的值为1;
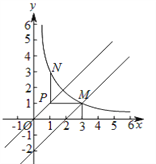
(2) ①当n=1时,P(1,1),令y=1,代入y=x-2,x-2=1,x=3,M(3,1),PM=2.
令x=1,代入![]() (x>0),y=3,N(1,3),PM=2, ∴PM=PN;
(x>0),y=3,N(1,3),PM=2, ∴PM=PN;
②∵P(n,n),点P在直线y=x上,过点P作平行于x轴的直线,交直线y=x-2于点M,M(n+2,n) , ∴PM=2,由题意知PN≥PM,即PN>2 ,∴0<n≤1或n≥3.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目