题目内容
 24、已知梯形ABCD中,AB∥CD,BD⊥AC于E,AD=BC,AC=AB,DF⊥AB于F,AC、DF相交于DF的中点O.
24、已知梯形ABCD中,AB∥CD,BD⊥AC于E,AD=BC,AC=AB,DF⊥AB于F,AC、DF相交于DF的中点O.(1)若点G为线段AB上一点,且FG=4,CD=3,GC=7,过O点作OH⊥GC于H,试证:OH=OF;
(2)求证:AB+CD=2BE.
分析:(1)连接OG.根据AAS可以证明△ODC≌△OFA,得AF=CD=3,则AG=7=CG.根据等腰三角形的三线合一,得OG为∠AGC的角平分线,根据角平分线的性质即可证明;
(2)过D作DM∥AC交BA的延长线于M,则四边形CDMA为平行四边形,得DM=AC,CD=AM,从而得到DMB为等腰直角三角形,根据等腰直角三角形的性质可以证明AM+AB=2BF;再结合全等三角形的性质即可证明.
(2)过D作DM∥AC交BA的延长线于M,则四边形CDMA为平行四边形,得DM=AC,CD=AM,从而得到DMB为等腰直角三角形,根据等腰直角三角形的性质可以证明AM+AB=2BF;再结合全等三角形的性质即可证明.
解答: 证明:(1)连接OG.
证明:(1)连接OG.
∵O为PF中点,
∴DO=OF,
又∵AB∥CD且DF⊥AB,
∴∠ODC=∠OFA.
∴在△ODC和△OFA中,
∴△ODC≌△OFA.
∴CD=AF=3.
又∵FG=4,
∴AG=AF+FG=7=CG.
即:AG=CG.
又∵△ODC≌△OFA,
∴OA=OC.
∵AG=CG,
∴OG为∠AGC的角平分线.
∵OF⊥AG,ON⊥CG,
∴OF=OH.
 (2)过D作DM∥AC交BA的延长线于M.
(2)过D作DM∥AC交BA的延长线于M.
∵梯形ABCS中,AD=BC,
∴BD=AC.
又∵CD∥AM,DM∥AC,
∴四边形CDMA为平行四边形.
∴DM=AC,CD=AM.
∵MD∥AC,又AC⊥BD,且AC=BD,
∴DM⊥BD,DM=BD,
∴△DMB为等腰直角三角形.
又∵DF⊥BM,
∴DF=BF.
∴BM=2DF=2BF
∴AM+AB=2BF.
∵CD=AM,
∴AB+CD=2BF.
∵AC=BD=AB,
∴在△BEA和△BFD中,△BEA≌△BFD.
∴BE=BF.
∵AB+CD=2BF,
∴AB+CD=2BE.
 证明:(1)连接OG.
证明:(1)连接OG.∵O为PF中点,
∴DO=OF,
又∵AB∥CD且DF⊥AB,
∴∠ODC=∠OFA.
∴在△ODC和△OFA中,
∴△ODC≌△OFA.
∴CD=AF=3.
又∵FG=4,
∴AG=AF+FG=7=CG.
即:AG=CG.
又∵△ODC≌△OFA,
∴OA=OC.
∵AG=CG,
∴OG为∠AGC的角平分线.
∵OF⊥AG,ON⊥CG,
∴OF=OH.
 (2)过D作DM∥AC交BA的延长线于M.
(2)过D作DM∥AC交BA的延长线于M.∵梯形ABCS中,AD=BC,
∴BD=AC.
又∵CD∥AM,DM∥AC,
∴四边形CDMA为平行四边形.
∴DM=AC,CD=AM.
∵MD∥AC,又AC⊥BD,且AC=BD,
∴DM⊥BD,DM=BD,
∴△DMB为等腰直角三角形.
又∵DF⊥BM,
∴DF=BF.
∴BM=2DF=2BF
∴AM+AB=2BF.
∵CD=AM,
∴AB+CD=2BF.
∵AC=BD=AB,
∴在△BEA和△BFD中,△BEA≌△BFD.
∴BE=BF.
∵AB+CD=2BF,
∴AB+CD=2BE.
点评:此题综合运用了等腰梯形的性质、全等三角形的判定及性质、平行四边形的判定及性质以及直角三角形的性质.

练习册系列答案
相关题目
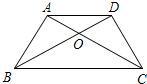 7、如图,已知梯形ABCD中,AD∥BC,AB=CD=AD,AC,BD相交于O点,∠BCD=60°,则下列说法错误的是( )
7、如图,已知梯形ABCD中,AD∥BC,AB=CD=AD,AC,BD相交于O点,∠BCD=60°,则下列说法错误的是( )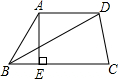 已知梯形ABCD中,AD∥BC,∠ABC=60°,BD=2
已知梯形ABCD中,AD∥BC,∠ABC=60°,BD=2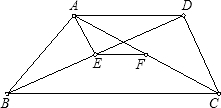 如图,已知梯形ABCD中,AD∥CB,E,F分别是BD,AC的中点,BD平分∠ABC.
如图,已知梯形ABCD中,AD∥CB,E,F分别是BD,AC的中点,BD平分∠ABC.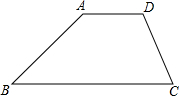 如图,已知梯形ABCD中,AD∥BC,∠B=40°,∠C=70°,AD=3,BC=7,则腰AB=
如图,已知梯形ABCD中,AD∥BC,∠B=40°,∠C=70°,AD=3,BC=7,则腰AB=