题目内容
 如图,已知梯形ABCD中,AD∥CB,E,F分别是BD,AC的中点,BD平分∠ABC.
如图,已知梯形ABCD中,AD∥CB,E,F分别是BD,AC的中点,BD平分∠ABC.(1)求证:AE⊥BD; (2)若AD=4,BC=14,求EF的长.
分析:(1)先由已知AD∥CB,得∠ADB=∠CBD,再由,BD平分∠ABC得∠ABD=∠CBD,由此推出∠ADB=∠ADB,即△ABD为等腰三角形,已知E,F分别是BD,AC的中点,所以推出AE⊥BD.
(2)延长AE交BC于G,能推出△ABE≌△GBE,所以得AE=GE,BG=AB,由(1)得AB=AD,则BG=AD,?CG=BC-BG=BC-AD,再由证明和已知得EF=
CG,从而求出EF的长.
(2)延长AE交BC于G,能推出△ABE≌△GBE,所以得AE=GE,BG=AB,由(1)得AB=AD,则BG=AD,?CG=BC-BG=BC-AD,再由证明和已知得EF=
| 1 |
| 2 |
解答:(1)证明:∵AD∥CB,
∴∠ADB=∠CBD,
又BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠ADB=∠ABD,
∴AB=AD,∴△ABD是等腰三角形,
已知E是BD的中点,
∴AE⊥BD.
(2)解:延长AE交BC于G,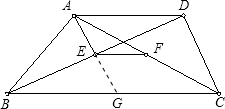
∵BD平分∠ABC,
∴∠ABE=∠GBE,
又∵AE⊥BD(已证),
∴∠AEB=∠GEB,
BE=BE,
∴△ABE≌△GBE,
∴AE=GE,BG=AB=AD,
又∵F是AC的中点(已知),
所以由三角形中位线定理得:
EF=
CG=
(BC-BG)=
(BC-AD)
=
×(14-4)=5.
答:EF的长为5.
∴∠ADB=∠CBD,
又BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠ADB=∠ABD,
∴AB=AD,∴△ABD是等腰三角形,
已知E是BD的中点,
∴AE⊥BD.
(2)解:延长AE交BC于G,

∵BD平分∠ABC,
∴∠ABE=∠GBE,
又∵AE⊥BD(已证),
∴∠AEB=∠GEB,
BE=BE,
∴△ABE≌△GBE,
∴AE=GE,BG=AB=AD,
又∵F是AC的中点(已知),
所以由三角形中位线定理得:
EF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
答:EF的长为5.
点评:此题考查的知识点是三角形中位线定理的应用和等腰三角形的判定和性质,其关键是(1)证△ABD是等腰三角形.(2)延长AE交BC于G,推出E是AG的中点和BG=AD.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
 9、如图,已知梯形ABCD中,AD∥BC,BE平分∠ABC,BE⊥CD,∠A=110°,AD=3,AB=5,则BC的长为( )
9、如图,已知梯形ABCD中,AD∥BC,BE平分∠ABC,BE⊥CD,∠A=110°,AD=3,AB=5,则BC的长为( )
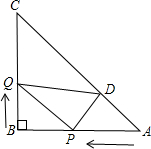 点到达终点时,另一点也随之停止.过Q作QD∥AB交AC于点D,连接PD,设运动时间为t秒时,四边形BQDP的面积为s.
点到达终点时,另一点也随之停止.过Q作QD∥AB交AC于点D,连接PD,设运动时间为t秒时,四边形BQDP的面积为s. (2007•遂宁)如图,已知等腰△ABC的面积为4cm2,点D、E分别是AB、AC边的中点,则梯形DBCE的面积为
(2007•遂宁)如图,已知等腰△ABC的面积为4cm2,点D、E分别是AB、AC边的中点,则梯形DBCE的面积为