题目内容
【题目】如图,△ABD与△AEC都是等边三角形,AB≠AC.下列结论中,正确的是 .
①BE=CD;②∠BOD=60°;③△BOD∽△COE.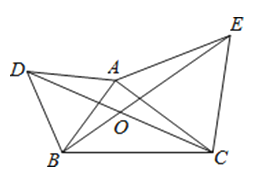
【答案】①②
【解析】解:∵△ABD与△AEC都是等边三角形,
∴AD=AB,AE=AC,∠ADB=∠ABD=60°,∠DAB=∠EAC=60°,
∴∠DAB+∠BAC=∠EAC+∠BAC,
∴∠DAC=∠BAE,
在△DAC和△BAE中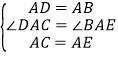 ,
,
∴△DAC≌△BAE(SAS),
∴BE=DC,∠ADC=∠ABE,
∵∠BOD=180°﹣∠ODB﹣∠DBA﹣∠ABE
=180°﹣∠ODB﹣60°﹣∠ADC
=120°﹣(∠ODB+∠ADC)
=120°﹣60°=60°,
∴∠BOD=60°,∴①正确;②正确;
∵△ABD与△AEC都是等边三角形,
∴∠ADB=∠AEC=60°,但根据已知不能推出∠ADC=∠AEB,
∴说∠BDO=∠CEO错误,
∴△BOD∽△COE错误,
∴③错误;
所以答案是:①②.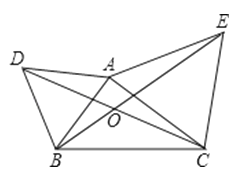
【考点精析】通过灵活运用相似三角形的判定,掌握相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS)即可以解答此题.

练习册系列答案
相关题目





