Question

【题目】定义：若一个三角形一条边上的高等于这条边长的一半，则称该三角形为“半高”三角形，这条高称为“半高”．

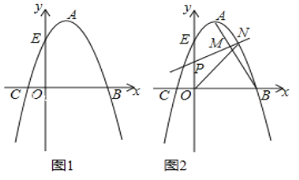
（1）如图1，中，，，点在上，于点，于点，连接，求证： 是“半高”三角形；

（2）如图2，是“半高”三角形，且边上的高是“半高”，点在上，交于点，于点，于点．

①请探究，，之间的等量关系，并说明理由；

②若的面积等于16，求的最小值．

Answer 1

【答案】（1）证明见解析；（2）①；②取得最小值．

【解析】

（1）根据平行相似，证明 ，利用相似三角形对应边的比等于对应高的比： ，由“半高”三角形的定义可结论；

（2）证明四边形 是矩形，得 ，代入，可得结论；

（3）先根据△ABC的面积等于16，计算BC和AR的长，设MN＝x，则 ，根据勾股定理表示MQ，配方可得最小值

解：（1）证明：由题意可证得，

∴，

∴，

由题意可证得四边形为矩形，∴，

∴，

∴是“半高”三角形．

（2）①．理由如下：

如图，过作于，交于，

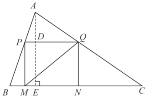
∵是“半高”三角形，且边上的高是“半高”，

∴

∵，

∴，

∴，

∴，

由题意可证得四边形是矩形，有，，

∴，

即．

②∵，故，

设，由①得，

∴，

∴当时，取得最小值．