题目内容
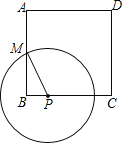
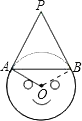
【题目】如图是不倒翁的正视图,不倒翁的圆形脸恰好与帽子边沿PA、PB分别相切于点A、B,不倒翁的鼻尖正好是圆心O.
(1)若∠OAB=25°,求∠APB的度数;
(2)若∠OAB=n°,请直接写出∠APB的度数.

【答案】(1)∠APB=50°;(2)∠APB=2n°.
【解析】
(1)连接OB,由AO=OB得,∠OAB=∠OBA=25°,∠AOB=180°-2∠BAB=130°;因为PA、PB分别相切于点A、B,则∠OAP=∠OBP=90°,所以∠APB=180°-∠AOB=50°.
(2)同(1)的解题思路一致,利用三角形内角和与四边形内角和推出结果.
解:(1)连接OB,
∵PA、PB切⊙O于A、B,
∴OA⊥PA,OP⊥AB,
∴∠OAP+∠OBP=180°,
∴∠APB+∠AOB=180°;
∵OA=OB,
∴∠OAB=∠OBA=25°,
∴∠AOB=130°,
∴∠APB=50°;
(2)连接OB,
∵PA、PB切⊙O于A、B,
∴OA⊥PA,OP⊥AB,
∴∠OAP+∠OBP=180°,
∴∠APB+∠AOB=180°;
∵OA=OB,
∴∠OAB=∠OBA=n°,
∴∠AOB=180°- 2n°,
∴∠APB=2n°.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目