题目内容
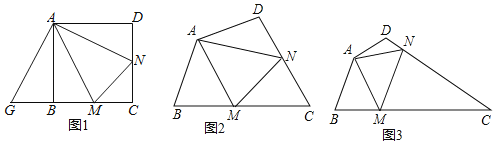
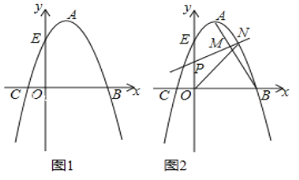
【题目】如图1,抛物线的顶点A的坐标为(1,4),抛物线与x轴相交于B、C两点,与y轴交于点E(0,3).
(1)求抛物线的表达式;
(2)已知点F(0,﹣3),在抛物线的对称轴上是否存在一点G,使得EG+FG最小,如果存在,求出点G的坐标;如果不存在,请说明理由.
(3)如图2,连接AB,若点P是线段OE上的一动点,过点P作线段AB的垂线,分别与线段AB、抛物线相交于点M、N(点M、N都在抛物线对称轴的右侧),当MN最大时,求△PON的面积.
【答案】(1)y=﹣x2+2x+3;(2)存在,G(1,0);(3)2.
【解析】
(1)根据顶点式可求得抛物线的表达式;
(2)根据轴对称的最短路径问题,作E关于对称轴的对称点E′,连接E′F交对称轴于G,此时EG+FG的值最小,先求E′F的解析式,它与对称轴的交点就是所求的点G;
(3)如图2,先利用待定系数法求AB的解析式,过N作NH⊥x轴于H,交AB于Q,设N(m,﹣m2+2m+3),则Q(m,﹣2m+6)(1<m<3),表示NQ=﹣m2+4m﹣3,证明△QMN∽△ADB,列比例式可得MN的表达式,根据配方法可得当m=2时,MN有最大值,证明△NGP∽△ADB,同理得PG的长,从而得OP的长,根据三角形的面积公式可得结论,并将m=2代入计算即可.
(1)设抛物线的表达式为:y=a(x﹣1)2+4,
把(0,3)代入得:3=a(0﹣1)2+4,
a=﹣1,
∴抛物线的表达式为:y=﹣(x﹣1)2+4=﹣x2+2x+3;
(2)存在,如图1,作E关于对称轴的对称点E',连接E'F交对称轴于G,此时EG+FG的值最小.
∵E(0,3),∴E'(2,3),
设EF的解析式为y=k′x+b′,
把F(0,﹣3),E'(2,3)分别代入,得![]() ,解得
,解得![]() ,
,
所以E'F的解析式为:y=3x﹣3,
当x=1时,y=3×1﹣3=0,∴G(1,0);
(3)如图2.
设AB的解析式为y=k″x+b″,
把A(1,4),B(3,0)分别代入,得![]() ,解得
,解得![]() ,
,
所以AB的解析式为:y=﹣2x+6,
过N作NH⊥x轴于H,交AB于Q,
设N(m,﹣m2+2m+3),则Q(m,﹣2m+6),(1<m<3),
∴NQ=(﹣m2+2m+3)﹣(﹣2m+6)=﹣m2+4m﹣3,
∵AD∥NH,∴∠DAB=∠NQM,
∵∠ADB=∠QMN=90°,∴△QMN∽△ADB,
∴![]() ,∴
,∴![]() ,
,
∴MN![]() (m﹣2)2
(m﹣2)2![]()
![]() 0,
0,
∴当m=2时,MN有最大值;
过N作NG⊥y轴于G,
∵∠GPN=∠ABD,∠NGP=∠ADB=90°,∴△NGP∽△ADB,
∴![]() ,∴PG
,∴PG![]() NG
NG![]() m,
m,
∴OP=OG﹣PG=﹣m2+2m+3![]() m=﹣m2
m=﹣m2![]() m+3,
m+3,
∴S△PON![]() OPGN
OPGN![]() (﹣m2
(﹣m2![]() m+3)m,
m+3)m,
当m=2时,S△PON![]() 2(﹣4+3+3)=2.
2(﹣4+3+3)=2.