题目内容
【题目】请你完成下面的证明：
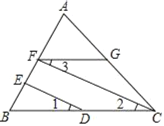
已知：如图，∠GFB+∠B＝180°，∠1＝∠3，
求证：FC∥ED．
证明：∵∠GFB+∠B＝180°
∴FG∥BC（ ）
∴∠3＝ （ ），
又∵∠1＝∠3（已知）
∴∠1＝ （等量代换）
∴FC∥ED（ ）
【答案】同旁内角互补，两直线平行；∠2；两直线平行，内错角相等；∠2；同位角相等，两直线平行．
【解析】
根据平行线的判定和性质，再根据等量代换得出∠1=∠2，再根据同位角相等，即可证明两直线平行．
证明：∵∠GFB+∠B=180°
∴FG∥BC（同旁内角互补，两直线平行）
∴∠3=∠2（两直线平行，内错角相等），
又∵∠1=∠3（已知）
∴∠1=∠2（等量代换）
∴FC∥ED（同位角相等，两直线平行）；
故答案为：同旁内角互补，两直线平行；∠2；两直线平行，内错角相等；∠2；同位角相等，两直线平行．
练习册系列答案
相关题目
【题目】某商贸公司有
、
两种型号的商品需运出，这两种商品的体积和质量分别如下表所示：
体积（立方米/件） | 质量（吨/件） | |
| 0．8 | 0．5 |
| 2 | 1 |
（1）已知一批商品有、两种型号，体积一共是20立方米，质量一共是10．5吨，求、两种型号商品各有几件？
（2）物资公司现有可供使用的货车每辆额定载重3．5吨，容积为6立方米，其收费方式有以下两种：
①按车收费：每辆车运输货物到目的地收费600元；
②按吨收费：每吨货物运输到目的地收费200元．
现要将（1）中商品一次或分批运输到目的地，如果两种收费方式可混合使用，商贸公司应如何选择运送、付费方式，使其所花运费最少，最少运费是多少元？