Question

【题目】问题提出

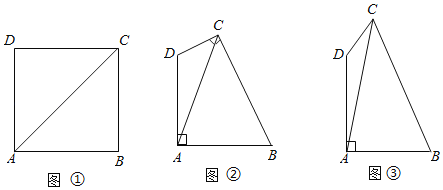
(1)如图①，在正方形ABCD中，对角线AC=8，则正方形ABCD的面积为　 　；

问题探究

(2)如图②，在四边形ABCD中，AD=AB，∠DAB=∠DCB=90°，∠ADC+∠ABC=180°，若四边形ABCD的面积为8，求对角线AC的长；

问题解决

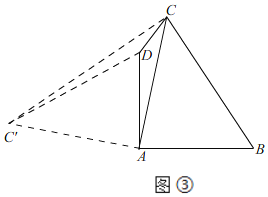
(3)如图③，四边形ABCD是张叔叔要准备开发的菜地示意图，其中边AD和AB是准备用砖来砌的砖墙，且满足AD=AB，∠DAB=90°，边DC和CB是准备用现有的长度分别为3米和7米的竹篱笆来围成的篱笆墙，即DC=3米，CB=7米．按照这样的想法，张叔叔围成的菜园里对角线AC的长是否存在最大值呢？若存在，求出这个最大值；若不存在，说明理由．

Answer 1

【答案】(1)32；(2)4；(3)存在，最大值为5．

【解析】

(1)先根据勾股定理求出AB的长，然后再根据面积公式解答即可；

(2)先说明△ADC'≌△ABC(SAS)，进而得出S△ADC'=S△ABC，AC'=AC，然后再根据面积公式解答即可；

(3先判断出点D在CC'上时， AC最大，求出AC的长即可．

解：(1)∵AC是正方形的对角线，

∴∠B=90°，AB=BC，

在Rt△ABC中，AC=8，

根据勾股定理得，AB2+BC2=AC2，

∴2AB2=AC2=64，

∴AB2=32，

∴S正方形ABCD=32，

故答案为32；

(2)如图②，延长CD至C'使DC'=BC，连接AC'，

∴∠ADC+∠ADC'=180°，

∵∠ADC+∠ABC=180°，

∴∠ADC'=∠ABC，

∵AD=AB，

∴△ADC'≌△ABC(SAS)，

∴S△ADC′=S△ABC，AC'=AC，

∴∠DAC'=∠BAC，

∴∠DAC'+∠CAD=∠BAC+∠CAD=∠BAD=90°，

∴∠CAC'=90°，

∵S四边形ABCD=S△ABC+S△ADC=S△ADC′+S△ADC=S△ACC′=8，

∵S△ACC′=ACAC'=AC2=8，

∴AC=4，

即AC的长为4；

(3)如图③，

将△ABC绕点A逆时针旋转90°得△ADC'，连接AC'，CC'，

由旋转知，AC'=AC，C'D=BC，∠CAC'=90°，

当点D在CC'上时，AC最大

此时，CC'=CD+C'D=CD+BC=10，

∴AC2=CC'2=50，

∴AC=5．