题目内容
【题目】如图，已知抛物线y=ax2+bx+c（a≠0）的顶点坐标为（4，﹣ 
），且与y轴交于点C（0，2），与x轴交于A，B两点（点A在点B的左边）．
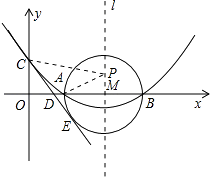
（1）求抛物线的解析式及A、B两点的坐标；
（2）在（1）中抛物线的对称轴l上是否存在一点P，使AP+CP的值最小？若存在，求AP+CP的最小值，若不存在，请说明理由；
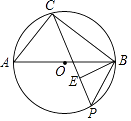
（3）以AB为直径的⊙M相切于点E，CE交x轴于点D，求直线CE的解析式．
【答案】
（1）
解：由题意，设抛物线的解析式为y=a（x﹣4）2﹣ 
（a≠0）
∵抛物线经过（0，2）
∴a（0﹣4）2﹣ =2
解得：a= 
∴y= （x﹣4）2﹣
即：y= x2﹣ 
x+2
当y=0时， x2﹣ x+2=0
解得：x=2或x=6
∴A（2，0），B（6，0）
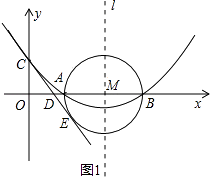
（2）
解：存在，
如图2，由（1）知：抛物线的对称轴l为x=4，
因为A、B两点关于l对称，连接CB交l于点P，则AP=BP，所以AP+CP=BC的值最小
∵B（6，0），C（0，2）
∴OB=6，OC=2
∴BC=2 
，
∴AP+CP=BC=2
∴AP+CP的最小值为2
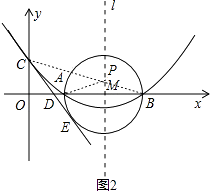
（3）
解：如图3，连接ME
∵CE是⊙M的切线
∴ME⊥CE，∠CEM=90°
∵C的坐标（0，2），
∴OC=2，
∵AB=4，
∴ME=2
∴OC=ME=2，
∵∠ODC=∠MDE，
∵在△COD与△MED中
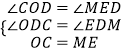
∴△COD≌△MED（AAS），
∴OD=DE，DC=DM
设OD=x
则CD=DM=OM﹣OD=4﹣x
则Rt△COD中，OD2+OC2=CD2，
∴x2+22=（4﹣x）2
∴x= 
∴D（ ，0）
设直线CE的解析式为y=kx+b（k≠0），
∵直线CE过C（0，2），D（ ，0）两点，
则 
解得：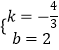 
∴直线CE的解析式为y=﹣ 
+2；
【解析】（1）利用顶点式求得二次函数的解析式后令其等于0后求得x的值即为与x轴交点坐标的横坐标；（2）线段BC的长即为AP+CP的最小值；（3）连接ME，根据CE是⊙M的切线得到ME⊥CE，∠CEM=90°，从而证得△COD≌△MED，设OD=x，在RT△COD中，利用勾股定理求得x的值即可求得点D的坐标，然后利用待定系数法确定线段CE的解析式即可．
